 |
A P. 5369. feladat (2021. december) |
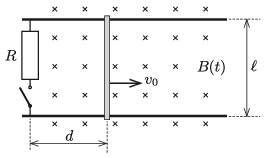
P. 5369. Vízszintes síkban \(\displaystyle \ell\) távolságban két párhuzamos fémsín található, melyek (ábra szerinti) bal oldali végét kapcsolóval ellátott \(\displaystyle R\) ellenállású fogyasztó köti össze. A rendszer függőleges irányú olyan homogén mágneses mezőben van, melyre jellemző mágneses indukcióvektor időben a \(\displaystyle B(t)=B_0+kt\) összefüggés szerint változik, ahol \(\displaystyle B_0\) és \(\displaystyle k\) ismert állandók. A sínekre merőlegesen egy fémpálcát fektetünk, amely a kapcsoló zárása előtt \(\displaystyle d\) távolságra van a fémsínek bal oldali végétől. A sínek és a fémpálca ellenállása elhanyagolható. A \(\displaystyle t = 0\) időpillanatban a kapcsolót zárjuk, és pálcát a vízszintes síkban, a pálcára merőlegesen \(\displaystyle v_0\) állandó sebességgel mozgatni kezdjük. Határozzuk meg a pálcában folyó áram erősségét a \(\displaystyle t\) időpillanatban!
Közli: Kotek László, Pécs
(5 pont)
A beküldési határidő 2022. január 17-én LEJÁRT.
Megoldás. Az adott elrendezésben egyszerre lép fel a nyugalmi és a mozgási indukció jelensége. A fémpálca a \(\displaystyle t\) időpillanatban \(\displaystyle d+v_0t\) távol van a kapcsolótól és az ellenállástól, tehát a pálca által képezett zárt hurok területe \(\displaystyle A(t)=(d+v_0t)\ell,\) aminek változási sebessége:
\(\displaystyle \frac{\Delta A}{\Delta t}=v_0\ell.\)
Ha ezt a változási sebességet megszorozzuk a mágneses indukció pillanatnyi értékével,
\(\displaystyle U_1=\frac{\Delta A}{\Delta t}\cdot B(t)=v_0\ell(B_0+kt)\)
indukált feszültséget kapunk. Ez a mozgási indukció járuléka.
Másrészt az \(\displaystyle A(t)\) területű téglalapon a mágneses indukció \(\displaystyle \frac{\Delta B(t)}{\Delta t}=k\) változási sebességével arányos feszültség jön létre:
\(\displaystyle U_2=k\cdot A(t)=k\ell(d+v_0t).\)
Ez a nyugalmi indukció járuléka.
A záródó vezetőben folyó áram erősségét a kétféle feszültség összege határozza meg:
\(\displaystyle I(t)=\frac{U_1+U_2}{R}=\frac{\ell}{R}(B_0v_0+kd+2kv_0t).\)
Statisztika:
38 dolgozat érkezett. 5 pontot kapott: Antalóczy Szabolcs, Bacsó Dániel, Barna Benedek, Bencz Benedek, Biebel Botond, Dóra Márton, Katona Attila Zoltán, Kürti Gergely, Molnár Kristóf, Mozolai Bende Bruno, Nemeskéri Dániel, Schmercz Blanka, Somlán Gellért, Téglás Panna, Toronyi András. 4 pontot kapott: Kertész Balázs, Yokota Adan. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 6 dolgozat.
A KöMaL 2021. decemberi fizika feladatai

