A P. 5393. feladat (2022. március)

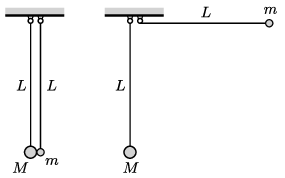
P. 5393. Egy \(\displaystyle m\) tömegű és egy \(\displaystyle M = 3m\) tömegű, kicsiny golyóhoz fonalakat erősítünk, melyek másik végét a bal oldali ábra szerint azonos magasságban rögzítjük. A golyók középpontja ekkor a felfüggesztés alatt \(\displaystyle L\) mélységben van. A kisebb tömegű golyót felemeljük úgy, hogy a hozzá kapcsolódó fonál vízszintes legyen (jobb oldali ábra), majd a golyót elengedjük. A két golyó tökéletesen rugalmasan és egyenesen ütközik.

\(\displaystyle a)\) Az ütközés előtti pillanatban mekkora együttes erővel terheli a két fonál a felfüggesztést?

\(\displaystyle b)\) Mekkora a terhelés az ütközés utáni pillanatban?

\(\displaystyle c)\) Az első és a második ütközés között mekkora a két fonál által bezárt legnagyobb szög?

\(\displaystyle d)\) A \(\displaystyle c)\) esetben mekkora nagyságú, és milyen irányú az együttes terhelés?

\(\displaystyle e)\) Mekkora szöget zárnak be a fonalak a függőlegessel, amikor bekövetkezik a második ütközés?

Közli: Zsigri Ferenc, Budapest

(5 pont)

A beküldési határidő 2022. április 19-én LEJÁRT.

Megoldás. \(\displaystyle a)\) Az energiamegmaradás törvénye szerint a kisebb golyó \(\displaystyle v=\sqrt{2gL}\) sebességgel mozog, a fonalat tehát a mozgásegyenlet szerint

\(\displaystyle N_1=mg+ma=mg+m\frac{v^2}{L}=3mg\)

erővel húzza. A másik, álló test által kifejtett erő

\(\displaystyle N_2=Mg=3mg.\)

A két fonál összesen \(\displaystyle 6mg\) nagyságú, függőlegesen lefelé ható erőt fejt ki a felfüggesztésre.

\(\displaystyle b)\) Az energia- és az impultusmegmaradás törvénye szerint az ütközés után a két golyó egymással ellentétes irányban,

\(\displaystyle v_1=\frac{v}{2}=\sqrt{\frac{gL}{2}} \)

nagyságú sebességgel kezd el mozogni. A fonalakat terhelő erők most:

\(\displaystyle N_1=mg+m\frac{v_1^2}{L}=\frac{3}{2}mg,\qquad \text{illetve} \qquad N_2=Mg+M\frac{v_1^2}{L}=\frac{3}{2}Mg=\frac{9}{2}mg.\)

A felfüggesztési pontot terhelő erő összesen

\(\displaystyle N_1+N_2=6mg,\)

éppen annyi, mint az ütközés előtt.

\(\displaystyle c)\) A \(\displaystyle v_1\) sebességgel elinduló testek a megállásukig \(\displaystyle h=\frac{v_1^2}{2g}=\frac{1}{4}L\) magasra emelkednek fel az ütközési pont magasságához viszonyítva. Mivel a két test kezdősebessége ugyanakkora, egyszerre állnak meg, és a fonaluknak a függőlegessel bezárt szöge

\(\displaystyle \varphi={\rm arccos}\,\frac{L-h}{L}={\rm arccos}\,\frac{3}{4}=41{,}4^\circ.\)

A két fonál által bezárt legnagyobb szög tehát \(\displaystyle 2\varphi=82{,}8^\circ\).

\(\displaystyle d)\) Amikor a testek pillanatnyi sebessége nulla, akkor a fonál irányú gyorsulásuk is nulla, tehát az egyes fonalakat

\(\displaystyle N_1=mg\cos\varphi=\frac{3}{4}mg, \qquad \text{illetve}\qquad N_2=Mg\cos\varphi=\frac{3}{4}Mg=\frac{9}{4}mg\)

nagyságú erő feszíti.

A felfüggesztésre ható eredő erő függőlegesen lefelé mutató komponense:

\(\displaystyle F_1=\left(N_1+N_2\right)\cos\varphi=\frac{9}{4}mg=2{,}25\ mg,\)

a vízszintes komponens pedig (ami a \(\displaystyle M\) tömegű golyó térfele irányába mutat)

\(\displaystyle F_2=\left(N_2-N_1\right)\sin\varphi=\frac{3 \sqrt{7}}{8}mg\approx 0{,}99\,mg.\)

Az eredő terhelés nagysága

\(\displaystyle F=\sqrt{F_1^2+F_2^2}=2{,}46\ mg,\)

iránya pedig

\(\displaystyle \alpha={\rm arctg}\,\frac{F_2}{F_1}=23{,}8^\circ\)

nagyságú szöget zár be a függőlegessel.

\(\displaystyle e)\) Mivel a fonálinga lengésideje nem függ a nehezék tömegétől, a második ütközés a fonalak függőleges, párhuzamos helyzeténél következik be.

Megjegyzés. A második ütközés után a golyók mozgása az előző mozgással egyezik meg, de ,,időben visszafelé''. A nagyobb tömegű golyó a második ütközés után megáll, a kisebb tömegű pedig \(\displaystyle v=\sqrt{2gL}\) sebességgel indul el, és egészen a fonál vízszintes helyzetéig lendül ki. (Mindez természetesen csak akkor igaz, ha az ütközések tökéletesen rugalmasak és a közegellenállás teljesen elhanyagolható.)

Statisztika:

42 dolgozat érkezett.
5 pontot kapott:	Antalóczy Szabolcs, Beke Bálint, Bencz Benedek, Dóra Márton, Gábriel Tamás, Kertész Balázs, Kovács Kristóf , Molnár Kristóf, Nemeskéri Dániel, Papp Marcell Imre, Pethő Dorottya, Schmercz Blanka, Somlán Gellért, Szabó Márton, Téglás Panna, Toronyi András, Vágó Botond, Varga Mária Krisztina, Vig Zsófia, Waldhauser Miklós.
4 pontot kapott:	Biebel Botond, Csonka Illés, Elekes Dorottya, Hauber Henrik, Hegedűs Máté Miklós, Kürti Gergely, Mészáros Ádám, Seprődi Barnabás Bendegúz.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2022. márciusi fizika feladatai