 |
A P. 5399. feladat (2022. március) |
P. 5399. Egy vékony, \(\displaystyle \delta\) vastagságú fémlemezből nagy, kúp alakú felületet hegesztettünk össze. A kúp \(\displaystyle A\)-val jelölt csúcsába \(\displaystyle I\) erősségű áramot vezetünk, majd az egyik alkotón lévő \(\displaystyle B\) pontból elvezetjük azt. Határozzuk meg a \(\displaystyle B\)-vel átellenes \(\displaystyle C\) pontban az áramsűrűség-vektor irányát és nagyságát! Ismert, hogy az \(\displaystyle AB\) távolság értéke \(\displaystyle 3R\), míg a \(\displaystyle B\) és \(\displaystyle C\) pontok távolsága \(\displaystyle 2R\).
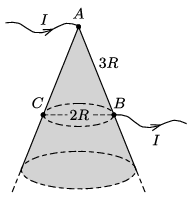
Közli: Vigh Máté, Biatorbány
(6 pont)
A beküldési határidő 2022. április 19-én LEJÁRT.
Megoldás. Az áramsűrűség olyan vektor, amely a töltések mozgásának irányába mutat, nagysága pedig a töltések mozgásirányára merőleges, egységnyi nagyságú felületen egységnyi idő alatt áthaladó töltések nagyságával egyezik meg.
Az egész elrendezés szimmetrikus az \(\displaystyle ABC\) síkra való tükrözésre, emiatt a \(\displaystyle C\) pontbeli áramsűrűség-vektor biztosan \(\displaystyle AC\) irányú. Ez annyit jelent, hogy az \(\displaystyle AC\) egyenesen keresztül sehol nem folyik áram, tehát a kúppalástot felvághatjuk az \(\displaystyle AC\) alkotója mentén, ettől nem változik meg az árameloszlás.
Terítsük ki síkba a felvágott fémlemezt! Mivel az \(\displaystyle AB\) távolság háromszor nagyobb, mint a \(\displaystyle CBC\) kör sugara, a kiterített fémlemez a teljes síknak egyharmada, \(\displaystyle 120^\circ\)-os szöget bezáró félegyenesek által határolt része lesz (1. ábra). Az ábrán a \(\displaystyle C\) pont két helyen is látható, a keresett áramsűrűség ezen két ponthoz tartozó áramsűrűségek összege.
1. ábra
Ha egy teljes (,,végtelen nagy'') sík \(\displaystyle A\) pontjába \(\displaystyle I\) erősségű áramot vezetünk, az szimmetrikusan fut szét, és az áramsűrűség nagysága az áram bevezetési pontjától \(\displaystyle r\) távolságban lévő \(\displaystyle P\) pontban
\(\displaystyle j_A(P)=\frac{I}{2\pi\delta}\,\frac{1}{r},\)
iránya pedig \(\displaystyle AP\)-vel párhuzamos. Amennyiben a végtelen sík egy másik, \(\displaystyle B\) pontjánál \(\displaystyle I\) erősségű áramot vezetünk ki a fémből, az áramsűrűség nagysága a \(\displaystyle P\) pontban
\(\displaystyle j_B(P)=-\frac{I}{2\pi\delta}\,\frac{1}{r'},\)
ahol \(\displaystyle r'=BP\), iránya pedig \(\displaystyle BP\)-vel párhuzamos. Az eredő árameloszlás áramsűrűség-vektora \(\displaystyle \boldsymbol j_A\) és \(\displaystyle \boldsymbol j_B\) összege, szuperpoziciója.
A felvágott és kiterített kúppalást esetében a szuperpozició még nem adja meg a helyes árameloszlást, hiszen nem teljesíti azt a feltételt, hogy az \(\displaystyle AC\) félegyenes áramvonal legyen. Egy kis kiegészítéssel azonban mégis célhoz érhetünk, ha alkalmazzuk (az elektrosztatikai tükörtöltésekre emlékeztető) ,,tüköráram-módszerét''. Helyezzünk el – gondolatban – a ténylegesen létező fémsíkdarab mellé két másik \(\displaystyle 120^\circ\)-os csúcsszögű síkharmadot, és ezek mindegyikének csúcspontjánál vezessünk be \(\displaystyle I\) erősségű áramot (összesen tehát \(\displaystyle 3I\)-t), a \(\displaystyle B'\) és \(\displaystyle B''\) pontoknál pedig ugyanekkora erősségű áramot vezessünk el a síkból (2. ábra). Az ábrán a három tartomány között – az áttekinthetőség kedvéért – egy kicsiny távolságot hagytunk, de ezt a számolás során nulla szélességűnek kell tekintenünk.
2. ábra
A síkharmad árameloszlását szuperponálva azt kapjuk, hogy a ténylegesen létező fémlemezben folyó árameloszlás olyan, mintha a végtelen sík \(\displaystyle A\) pontjába \(\displaystyle 3I\) erősségű áramot vezetnénk be, a \(\displaystyle B\), \(\displaystyle B'\) és \(\displaystyle B''\) pontoknál pedig \(\displaystyle I\)-t ki. Az elrendezés szimmetriája miatt a síkharmadokat határoló félegyenesek mindegyike áramvonal, tehát az eredeti fémlemezre vonatkozó határfeltétel valóban teljesül.
A \(\displaystyle C\) pontban az eredő áramsűrűség a 3. ábra szerint
\(\displaystyle \boldsymbol j(C)=\boldsymbol j_A(C)+\boldsymbol j_B(C)+\boldsymbol j_{B'}(C)+\boldsymbol j_{B''}(C),\)
ahol a vektorok nagysága:
\(\displaystyle j_A(C)=\frac{3I}{2\pi\delta}\,\frac{1}{3R},\qquad j_{B}(C)=j_{B''}(C)=\frac{I}{2\pi\delta}\,\frac{1}{3R} \qquad\text{és}\qquad j_{B'}(C)=\frac{I}{2\pi\delta}\,\frac{1}{6R}.\)
3. ábra
Az eredő áramsűrűség nagysága (az egyes összetevők irányát is figyelembe véve):
\(\displaystyle j(C)=j_A(C)-\frac{1}{2}j_{B}(C)-\frac{1}{2}j_{B''}(C)-j_{B'}(C)=\frac{I}{4\pi\delta R},\)
iránya pedig \(\displaystyle A\)-ból \(\displaystyle C\) felé mutat.
Statisztika:
6 dolgozat érkezett. 6 pontot kapott: Gábriel Tamás, Toronyi András. 5 pontot kapott: Téglás Panna. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2022. márciusi fizika feladatai