A P. 5411. feladat (2022. május)

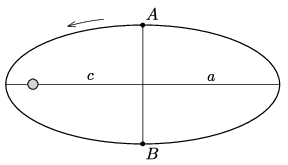
P. 5411. A Föld körül egy műhold \(\displaystyle c/a=e\) numerikus excentricitású ellipszispályán kering, keringési ideje \(\displaystyle T\). Mennyi idő alatt ér a műhold az ábrán jelölt \(\displaystyle A\) pontból a \(\displaystyle B\) pontba?

Közli: Szász Krisztián, Budapest

(4 pont)

A beküldési határidő 2022. június 15-én LEJÁRT.

Megoldás. Kepler II. törvénye szerint a műhold mozgásának \(\displaystyle T_{AB}\) ideje a vezérsugár által súrolt területtel arányos. Ha az ellipszis fél kistengelye \(\displaystyle b\), akkor az ellipszis teljes területe \(\displaystyle ab\pi\). A Kepler-törvény szerint

\(\displaystyle \frac{T_{AB}}{T}=\frac{\tfrac12ab\pi-bc}{ab\pi}=\frac12-\frac{c}{a\pi},\)

tehát

\(\displaystyle T_{AB}=\left(\frac12-\frac{e}{\pi}\right)T.\)

Statisztika:

25 dolgozat érkezett.
4 pontot kapott:	Dóra Márton, Gábriel Tamás, Hauber Henrik, Hegedűs Máté Miklós, Horváth 221 Zsóka, Kertész Balázs, Kovács Kristóf , Mészáros Ádám, Papp Marcell Imre, Pethő Dorottya, Schmercz Blanka, Seprődi Barnabás Bendegúz, Somlán Gellért, Tárnok Ede , Toronyi András, Vágó Botond, Vig Zsófia, Waldhauser Miklós.
3 pontot kapott:	Beke Bálint, Bencz Benedek, Katona Attila Zoltán, Nemeskéri Dániel.
2 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2022. májusi fizika feladatai