A P. 5414. feladat (2022. május)

P. 5414. Fémdrótból egy \(\displaystyle R\) sugarú kört formáztunk, és ugyanebből a drótból az egyik átmérőt is elkészítettük. Mekkora legyen az \(\displaystyle AB = AC\) ívek hossza, hogy az \(\displaystyle A\) és \(\displaystyle B\) pontok között mérhető eredő ellenállás megegyezzen a \(\displaystyle B\) és \(\displaystyle C\) pontok között mérhető eredő ellenállással?

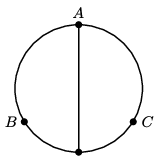
Közli: Gáspár Merse Előd, Budapest

(4 pont)

A beküldési határidő 2022. június 15-én LEJÁRT.

Megoldás. Legyen az \(\displaystyle AB\) és az \(\displaystyle AC\) ívek hossza \(\displaystyle xR\), vagyis a kör sugarának \(\displaystyle x\)-szerese. Az egyes drótdarabok ellenállása a hosszukkal arányos. Válasszunk olyan mértékegységrendszert, amelyben az \(\displaystyle AD\) átmérő menti drót ellenállása 2 egység, és ennek megfelelően az \(\displaystyle AB\) és \(\displaystyle AC\) drótívek ellenállása \(\displaystyle x\), a \(\displaystyle BD\) és \(\displaystyle CD\) ívek ellenállása pedig \(\displaystyle \pi-x\) lesz, ahogy azt az ábra mutatja. (Az ábrán látható számok nem hosszúságokat, hanem a megfelelő drótdarab ellenállását jelölik.) Az \(\displaystyle AB\) és a \(\displaystyle BC\) pontok között mérhető ellenállások aránya nem függ az ellenállás önkényesen választott mértékegységétől, tehát ezek az új egységekkel számolva is egyenlő nagyságúak maradnak.

Ha a \(\displaystyle B\) és a \(\displaystyle C\) pont között mérünk ellenállást, a szimmetria miatt az \(\displaystyle A\) és a \(\displaystyle D\) pontok ekvipotenciálisak lesznek, és emiatt a közöttük lévő egyenes drótdarabot kiiktathatjuk. A mért ellenállás egy \(\displaystyle 2x\) nagyságú és egy \(\displaystyle 2(\pi-x)\) nagyságú, párhuzamosan kapcsolt ellenállás eredője lesz:

\(\displaystyle R_{BC}=\left(\frac{1}{2x}+\frac{1}{2(\pi-x)}\right)^{-1}.\)

Bonyolultabb a helyzet az \(\displaystyle A\) és \(\displaystyle B\) pontok közötti ellenállás kiszámításánál. Az \(\displaystyle A\) és a \(\displaystyle D\) pont közötti egyenes, illetve félkör alakú vezeték párhuzamos eredője:

\(\displaystyle \left(\frac{1}{2}+\frac{1}{\pi}\right)^{-1}=\frac{2\pi}{2+\pi}.\)

Ehhez csatlakozik sorosan kapcsolva a \(\displaystyle BD\) ív \(\displaystyle \pi-x\) nagyságú ellenállása, majd párhuzamosan az \(\displaystyle AB\) ív \(\displaystyle x\) nagyságú ellenállása. Így tehát

\(\displaystyle R_{AB}= \left(\frac{1}{\pi-x+\frac{2\pi}{2+\pi}}+\frac{1}{x}\right)^{-1}.\)

Az \(\displaystyle R_{BC}=R_{AB}\) feltétel szerint fennáll az

\(\displaystyle \frac{1}{2x}+\frac{1}{2(\pi-x)}=\frac{1}{\pi-x+\frac{2\pi}{2+\pi}}+\frac{1}{x}\)

összefüggés, amiből algebrai átalakítások után a

\(\displaystyle (6+\pi)x=\pi(4+\pi)\)

lineáris egyenletet kapjuk. Ennek megoldása:

\(\displaystyle x=\frac{4+\pi}{6+\pi}\pi \approx 2{,}45.\)

Ezek szerint az \(\displaystyle AB\) és az \(\displaystyle AC\) ívek hossza

\(\displaystyle \frac{\pi(4+\pi)}{6+\pi}R \approx 2{,}45\,R.\)

Statisztika:

23 dolgozat érkezett.
4 pontot kapott:	Csonka Illés, Gábriel Tamás, Hauber Henrik, Horváth 221 Zsóka, Kovács Kinga, Molnár Kristóf, Pethő Dorottya, Schmercz Blanka, Somlán Gellért, Téglás Panna, Veszprémi Rebeka Barbara, Vig Zsófia.
3 pontot kapott:	Bogdán Benedek, Dóra Márton, Hegedűs Máté Miklós, Szabó Márton, Tárnok Ede , Toronyi András.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2022. májusi fizika feladatai