A P. 5415. feladat (2022. május)

P. 5415. Egy elhanyagolható ellenállású, szigetelés nélküli huzalból, a vízszintes síkban elhelyezkedő, $\displaystyle \alpha= 45^\circ$-os szöget bezáró, V alakot hajlítunk. Ezt az elrendezést olyan mágneses mezőbe helyezzük, melynek $\displaystyle \boldsymbol B$ indukcióvektora merőleges a vízszintes síkra, és nagysága a $\displaystyle B(t) = B_0/t_0\cdot t$ összefüggés szerint változik az időben, ahol $\displaystyle B_0$ és $\displaystyle t_0$ ismert állandók. A V alakú vezetőre szigetelés nélküli, kezdetben rögzített fémrudat helyezünk az ábrának megfelelő módon. A rúd egységnyi hosszúságú darabjának ellenállása $\displaystyle r$.

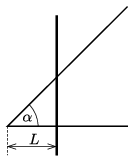
$\displaystyle a)$ Mennyi hő fejlődik a fémrúdban $\displaystyle t_0$ idő alatt?

$\displaystyle b)$ A bekapcsolástól ($\displaystyle t = 0$ időpillanat) számított $\displaystyle t_0$ időpillanatban a mágneses indukció változása megszűnik. Ebben a pillanatban az eddig rögzített fémrudat a vízszintes síkban, a fémrúdra merőlegesen $\displaystyle v_0$ sebességgel mozgatni kezdjük. Mekkora legyen ez a sebesség, hogy a rúdban folyó áram erőssége ne változzon?

$\displaystyle c)$ Hányszor több hő fejlődik a fémrúdban a mozgatás során, mint a rögzített helyzetben, ha a fémrudat $\displaystyle 2t_0$ hosszú ideig mozgatjuk?

Közli: Kotek László, Pécs

(5 pont)

A beküldési határidő 2022. június 15-én LEJÁRT.

Megoldás. $\displaystyle a)$ A derékszögű háromszög területe $\displaystyle L^2/2$, a rajta áthaladó mágneses fluxus

$\displaystyle \Phi=\frac{L^2}{2}\cdot B(t)=\frac{L^2}{2}\cdot\frac{B_0}{t_0}t,$

a fluxus változásnak sebessége, vagyis a nyugalmi indukció folytán indukálódó feszültség:

$\displaystyle U=\frac{\Delta \Phi}{\Delta t}=\frac{B_0L^2}{2t_0}.$

Az $\displaystyle L$ hosszúságú vezető ellenállása $\displaystyle Lr$, így az áramerősség

$\displaystyle I=\frac{U}{R}=\frac{B_0L}{2t_0r},$

vagyis a $\displaystyle t_0$ idő alatt fejlődő hő

$\displaystyle Q_1=UIt_0 ={I^2}Rt_0=\frac{B_0^2L^3}{4t_0r}.$

$\displaystyle b)$ A $\displaystyle B_0$ erősségű mágneses térben mozgó vezetőben a mozgási indukció folytán feszültség indukálódik. A vezetőnek a V alakú huzal közötti része $\displaystyle t$ idővel a mozgás kezdete után $\displaystyle L+v_0t$, így az indukált feszültség

$\displaystyle U(t)=B_0(L+v_0t)v_0,$

az áramerősség pedig

$\displaystyle I(t)=\frac{U(t)}{R(t)}=\frac{B_0(L+v_0t)v_0}{(L+v_0t)r}=\frac{B_0v_0}{r}.$

(Látható, hogy az áramerősség időben nem változik.)

A még mozdulatlan és a már mozgó fémrúdban az áramerősség ugyanakkora:

$\displaystyle \frac{B_0L}{2t_0r}=\frac{B_0v_0}{r}, \qquad \text{vagyis}\qquad v_0=\frac{L}{2t_0}.$

$\displaystyle c)$ A fémrúd áramot vezető részének hossza az induláskor $\displaystyle L$, $\displaystyle 2t_0$ idővel később $\displaystyle L+2v_0t_0=2L$. Így a vezető ellenállása időben egyenletesen $\displaystyle Lr$-ről $\displaystyle 2Lr$-re növekszik, a hőfejlődés teljesítménye pedig $\displaystyle P_1=I^2R_1$-ről $\displaystyle P_2=I^2R_2=2P_1$ nagyságúra változik. Mivel a változás egyenletes, számolhatunk az átlagteljesítménnyel, és így a $\displaystyle 2t_0$ idő alatt fejlődő hő összesen

$\displaystyle Q_2=2t_0\frac{P_1+P_2}{2}=\frac{3B_0^2L^3}{4t_0r}=3Q_1.$

A mozgatás során tehát 3-szor több hő fejlődik a fémrúdban, mint a rögzített helyzetben.

Statisztika:

15 dolgozat érkezett.
5 pontot kapott:	Gábriel Tamás, Kertész Balázs, Molnár Kristóf, Somlán Gellért, Téglás Panna, Toronyi András, Veszprémi Rebeka Barbara.
4 pontot kapott:	Hegedűs Máté Miklós, Nemeskéri Dániel.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	3 versenyző.

A KöMaL 2022. májusi fizika feladatai