 |
A P. 5447. feladat (2022. december) |
P. 5447. Három egyforma, 5 cm sugarú jéghengert készítünk, és azokat az ábrán látható helyzetből kezdősebesség nélkül elengedjük. A súrlódás mindenhol elhanyagolható.
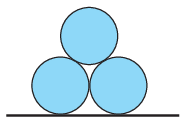
Mekkora gyorsulással indulnak el a jéghengerek?
Közli: Cserti József, Budapest
(5 pont)
A beküldési határidő 2023. január 16-án LEJÁRT.
Megoldás. Tekintsük azt a helyzetet, amikor az alsó két jéghenger már egy nagyon kicsit eltávolodott egymástól, és használjuk az ábra jelöléseit.
A felső henger \(\displaystyle A\) tengelye éppen akkora gyorsulással mozog a másik henger \(\displaystyle B\) tengelye felé, amennyivel \(\displaystyle B\) távolodik \(\displaystyle A\)-tól, hiszen a közöttük lévő távolság állandó. Ezek szerint
\(\displaystyle a_1\cos\beta=a_2\cos\alpha.\)
Mivel az indulás pillanatában \(\displaystyle \alpha=60^\circ\) és \(\displaystyle \beta=30^\circ\), a fenti ,,kényszerfeltétel'' szerint
\(\displaystyle a_2=\sqrt3\,a_1.\)
Az indulást követő nagyon rövid \(\displaystyle t\) idő alatt az \(\displaystyle m\) tömegű felső henger lesüllyed \(\displaystyle a_1t^2/2\)-vel, és a sebessége \(\displaystyle a_1t\) lesz. A vízszintesen (szimmetrikusan) szétcsúszó alsó hengerek sebessége \(\displaystyle a_2t\) lesz. Az energiamegmaradás tétele szerint
\(\displaystyle mg\dfrac{a_1}{2}t^2= \dfrac{1}{2}m(a_1t)^2+2\cdot \dfrac{1}{2}m(a_2t)^2,\)
vagyis (a kényszerfeltételt is kihasználva)
\(\displaystyle a_1g=a_1^1+2a_2^2=7a_1^2.\)
Így a kérdéses gyorsulások:
\(\displaystyle a_1=\frac17\,g\approx 1{,}4~\frac{\rm m}{\rm s^2}, \qquad \text{illetve} \qquad a_2=\dfrac{\sqrt3}{7}\,g\approx 2{,}4~\frac{\rm m}{\rm s^2}.\)
Az eredmény sem a jéghengerek méretétől, sem a tömegüktől nem függ.
Statisztika:
48 dolgozat érkezett. 5 pontot kapott: Bencz Benedek, Bodré Zalán, Chrobák Gergő, Csilling Dániel, Halász Henrik, Kovács Kristóf , Nagy 456 Imre, Nemeskéri Dániel, Vágó Botond, Vincze Farkas Csongor, Waldhauser Miklós. 4 pontot kapott: Halász Sámuel, Klement Tamás. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 8 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 9 dolgozat.
A KöMaL 2022. decemberi fizika feladatai