 Problem P. 5462. (January 2023)
Problem P. 5462. (January 2023)
P. 5462. A long rod is attached to a spring of negligible mass. If the spring is suspended by the other end, its elongation will be \(\displaystyle s=15\) cm. Then the spring and the rod are placed on a horizontal, frictionless surface and the free end of the spring is fixed. The rod is pulled back by a distance of \(\displaystyle \ell\) as shown in the figure, so the spring will be stretched. Finally, a cube-shaped body is placed on the top face of the rod, at that end of the rod which is closer to the spring. The coefficient of friction (both static and dynamic) between the rod and the cube is \(\displaystyle \mu=0.2\).
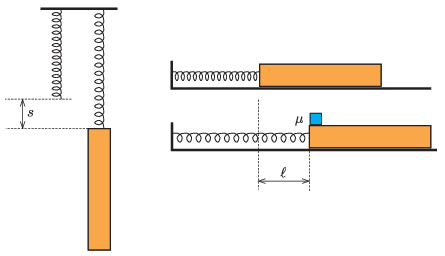
When the rod is released, the system starts to move and the cube slides on the rod. The sliding between the two bodies ceases after the moment when the acceleration of the cube becomes zero.
\(\displaystyle a)\) How long did the cube slide on the rod?
\(\displaystyle b)\) What is the least distance of \(\displaystyle \ell\) in order that the above described motion could occur?
\(\displaystyle c)\) How much distance did the cube slide along the rod?
(6 pont)
Deadline expired on February 15, 2023.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás.Jelöljük a rugó direkciós erejét \(\displaystyle D\)-vel, a hasáb tömegét \(\displaystyle M\)-mel, a kocka tömegét \(\displaystyle m\)-mel. A függőlegesen tartott rugónál a hasáb egyensúlyának feltétele:
| \(\displaystyle (1)\) | \(\displaystyle Mg=Ds.\) |
Tételezzük fel egy pillanatra, hogy a hasáb elengedésekor a kocka nem kezd el csúszni, hanem együtt mozog a hasábbal. A két test \(\displaystyle a\) gyorsulását a \(\displaystyle D\ell\) rugóerő okozza:
\(\displaystyle D\ell=(M+m)a, \qquad \text{tehát}\qquad a=\dfrac{D\ell}{M+m}.\)
A súrlódási erő, ami a testek között hat (a hasábot fékezi, a kocka alakú testet gyorsítja) nem lehet nagyobb, mint \(\displaystyle \mu mg\), tehát a kocka maximális gyorsulása (amikor nem csúszik a hasábon) \(\displaystyle a_{\rm max}=\mu g\). A kis test tehát csak akkor nem csúszik meg a hasábon, ha
\(\displaystyle \dfrac{D\ell}{M+m}\le \mu g, \qquad \text{vagyis}\qquad\ell\le \dfrac{\mu g}{D}(M+m).\)
Ha ez a feltétel nem teljesül, hanem
| \(\displaystyle (2)\) | \(\displaystyle \ell> \dfrac{\mu g}{D}(M+m),\) |
a kis test ,,lemarad'' a hasábhoz képes, tehát elcsúszik azon. A továbbiakban feltételezzük, hogy ez következik be, és a (2) egyenlőtlenség teljesülését majd később ellenőrizzük.
\(\displaystyle a)\) Legyen a hasáb távolsága a nyújtatlan rugó végpontjától \(\displaystyle x(t)\), a kocka távolsága pedig \(\displaystyle y(t)\). (Az időt a hasáb elengedésének pillanatától kezdődően mérjük.) Mivel a rugóerő ilyenkor \(\displaystyle -Dx\), a súrlódási erő pedig \(\displaystyle \mu mg\), a két test mozgásegyenlete:
\(\displaystyle Ma_x=-D x+\mu mg,\)
ami így is felírható:
| \(\displaystyle (3)\) | \(\displaystyle Ma_x=-D \left(x -\frac{\mu mg}D\right), \) |
továbbá
| \(\displaystyle (4)\) | \(\displaystyle ma_y=-\mu mg.\) |
Látható, hogy az \(\displaystyle x -\frac{\mu mg}D\) változóra a harmonikus rezgőmozgás egyenlete áll fenn, amelynek megoldása (az \(\displaystyle x(0)=\ell\) és \(\displaystyle v_x(0)=0\) kezdeti feltételeket is figyelembe véve):
| \(\displaystyle (5)\) | \(\displaystyle x(t)=\frac{\mu mg}D+\left(\ell-\frac{\mu mg}D\right)\cos(\omega t),\) |
ahol
| \(\displaystyle (6)\) | \(\displaystyle \omega=\sqrt{\dfrac{D}{M}},\) |
továbbá a hasáb sebessége
| \(\displaystyle (7)\) | \(\displaystyle v_x(t)=-\left(\ell-\frac{\mu mg}D\right)\omega\sin(\omega t).\) |
A (3) egyenlet könnyebben megoldható, hiszen az egy egyenletesen gyorsuló test mozgásegyenlete:
| \(\displaystyle (8)\) | \(\displaystyle y(t)=\ell-\dfrac{\mu g}{2}t^2,\) |
a kocka pillanatnyi sebessége pedig:
| \(\displaystyle (9)\) | \(\displaystyle v_y(t)=- \mu gt.\) |
A hasáb gyorsulása negyed rezgés után csökken nullára:
| \(\displaystyle (10)\) | \(\displaystyle t_0=\dfrac{T}{4}=\dfrac{\pi}{2}\sqrt{\dfrac{M}{D}},\) |
ami (1) alapján így is írható:
\(\displaystyle t_0=\dfrac{\pi}{2}\sqrt{\dfrac{s}{g}}=0{,}2\ \rm s.\)
\(\displaystyle b)\) A csúszás akkor szűnik meg, amikor a két test sebessége megegyezik:
\(\displaystyle v_x(t_0)=v_y(t_0),\)
ahonnan (6), (7), (9) és (10) felhasználásával kapjuk, hogy
\(\displaystyle \ell=\dfrac{\mu gM}{D}\left(\dfrac{\pi}{2}+\dfrac{m}{M}\right).\)
Innen látszik, hogy a (2) feltétel biztosan teljesül, hiszen \(\displaystyle \pi/2>1\). Az \(\displaystyle m\) tömeg nagyságát nem ismerjük, de biztosan igaz, hogy \(\displaystyle m>0\), ennek megfelelően
\(\displaystyle \ell>\dfrac{\pi}{2}\cdot \dfrac{\mu M g}{D}=\dfrac{\pi}{2}\,\mu s=0{,}047\ {\rm m} \approx 5\ \rm cm.\)
\(\displaystyle c)\) A kockának a hasábhoz viszonyított elmozdulása (tehát a csúszásának hossza) \(\displaystyle t_0\) idő alatt
\(\displaystyle \Delta s=y(t_0)-x(t_0), \)
ami (5), (8) és (10) szerint
\(\displaystyle \Delta s=\mu s\left[\left(\dfrac{\pi}{2}+\dfrac{m}{M}\right)-\dfrac{\pi^2 }8\right] -\mu s\dfrac{m}{M}=\mu s \left( \dfrac{\pi}{2} -\dfrac{\pi^2 }8\right)\approx 1\ \rm cm.\)
(Érdekes, hogy \(\displaystyle \Delta s\) nem függ a kocka \(\displaystyle m\) tömegétől, emiatt nem okozott problémát, hogy annak nagysága nem szerepelt a megadott számadatok között.)
Megjegyzés. Belátható, hogy a csúszás megszűnte után, amikor a hasáb és a kocka egyetlen testként mozog, a kockára ható (vízszintes) erő nem haladja meg a \(\displaystyle \mu mg\) kritikus értéket, tehát a továbbiakban semmikor nem kezd újra csúszni.
A csúszás megszűntének pillanatában mind a hasáb, mind pedig a kocka gyorsulása ugrásszerűen megváltozik, a közös gyorsulásuk a tömegközéppont korábbi gyorsulásával egyezik meg.
Statistics:
11 students sent a solution. 6 points: Bencz Benedek, Flóring Balázs, Molnár Kristóf, Szabó Zsombor. 3 points: 3 students. 2 points: 1 student. 1 point: 2 students.
Problems in Physics of KöMaL, January 2023
