 |
A P. 5462. feladat (2023. január) |
P. 5462. Elhanyagolható tömegű rugóhoz hosszú hasábot erősítünk. Ha a rugót a másik végénél fogva felfüggesztjük, megnyúlása \(\displaystyle s=15\) cm lesz. Ezután a rugót és a hasábot vízszintes, súrlódásmentes síkra helyezzük, és a rugó szabad végét rögzítjük. A hasábot az ábrán látható módon \(\displaystyle \ell\) távolsággal hátrahúzzuk, így a rugó megnyúlik. Végül a hasáb felső lapjára, annak rugó felőli végére egy kocka alakú testet helyezünk. A hasáb és a kocka közötti (tapadási és csúszási) súrlódási együttható \(\displaystyle \mu=0{,}2\).
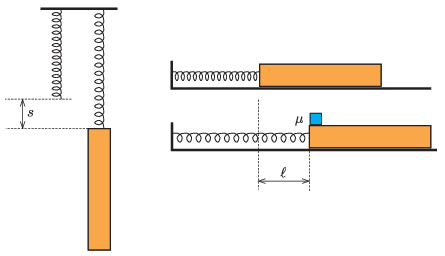
Ha a hasábot elengedjük, a rendszer mozgásba jön, és a kocka elcsúszik a hasábon. A két test közötti csúszás azt a pillanatot követően szűnik meg, amikor a hasáb gyorsulása nullává válik.
\(\displaystyle a)\) Mennyi ideig csúszott a kocka a hasábon?
\(\displaystyle b)\) Legalább mekkora az \(\displaystyle \ell\) távolság, ha a leírt mozgás létrejöhetett?
\(\displaystyle c)\) Mekkora távolsággal csúszott el a kocka a hasábon?
Közli:Wiedemann László, Budapest
(6 pont)
A beküldési határidő 2023. február 15-én LEJÁRT.
Megoldás.Jelöljük a rugó direkciós erejét \(\displaystyle D\)-vel, a hasáb tömegét \(\displaystyle M\)-mel, a kocka tömegét \(\displaystyle m\)-mel. A függőlegesen tartott rugónál a hasáb egyensúlyának feltétele:
| \(\displaystyle (1)\) | \(\displaystyle Mg=Ds.\) |
Tételezzük fel egy pillanatra, hogy a hasáb elengedésekor a kocka nem kezd el csúszni, hanem együtt mozog a hasábbal. A két test \(\displaystyle a\) gyorsulását a \(\displaystyle D\ell\) rugóerő okozza:
\(\displaystyle D\ell=(M+m)a, \qquad \text{tehát}\qquad a=\dfrac{D\ell}{M+m}.\)
A súrlódási erő, ami a testek között hat (a hasábot fékezi, a kocka alakú testet gyorsítja) nem lehet nagyobb, mint \(\displaystyle \mu mg\), tehát a kocka maximális gyorsulása (amikor nem csúszik a hasábon) \(\displaystyle a_{\rm max}=\mu g\). A kis test tehát csak akkor nem csúszik meg a hasábon, ha
\(\displaystyle \dfrac{D\ell}{M+m}\le \mu g, \qquad \text{vagyis}\qquad\ell\le \dfrac{\mu g}{D}(M+m).\)
Ha ez a feltétel nem teljesül, hanem
| \(\displaystyle (2)\) | \(\displaystyle \ell> \dfrac{\mu g}{D}(M+m),\) |
a kis test ,,lemarad'' a hasábhoz képes, tehát elcsúszik azon. A továbbiakban feltételezzük, hogy ez következik be, és a (2) egyenlőtlenség teljesülését majd később ellenőrizzük.
\(\displaystyle a)\) Legyen a hasáb távolsága a nyújtatlan rugó végpontjától \(\displaystyle x(t)\), a kocka távolsága pedig \(\displaystyle y(t)\). (Az időt a hasáb elengedésének pillanatától kezdődően mérjük.) Mivel a rugóerő ilyenkor \(\displaystyle -Dx\), a súrlódási erő pedig \(\displaystyle \mu mg\), a két test mozgásegyenlete:
\(\displaystyle Ma_x=-D x+\mu mg,\)
ami így is felírható:
| \(\displaystyle (3)\) | \(\displaystyle Ma_x=-D \left(x -\frac{\mu mg}D\right), \) |
továbbá
| \(\displaystyle (4)\) | \(\displaystyle ma_y=-\mu mg.\) |
Látható, hogy az \(\displaystyle x -\frac{\mu mg}D\) változóra a harmonikus rezgőmozgás egyenlete áll fenn, amelynek megoldása (az \(\displaystyle x(0)=\ell\) és \(\displaystyle v_x(0)=0\) kezdeti feltételeket is figyelembe véve):
| \(\displaystyle (5)\) | \(\displaystyle x(t)=\frac{\mu mg}D+\left(\ell-\frac{\mu mg}D\right)\cos(\omega t),\) |
ahol
| \(\displaystyle (6)\) | \(\displaystyle \omega=\sqrt{\dfrac{D}{M}},\) |
továbbá a hasáb sebessége
| \(\displaystyle (7)\) | \(\displaystyle v_x(t)=-\left(\ell-\frac{\mu mg}D\right)\omega\sin(\omega t).\) |
A (3) egyenlet könnyebben megoldható, hiszen az egy egyenletesen gyorsuló test mozgásegyenlete:
| \(\displaystyle (8)\) | \(\displaystyle y(t)=\ell-\dfrac{\mu g}{2}t^2,\) |
a kocka pillanatnyi sebessége pedig:
| \(\displaystyle (9)\) | \(\displaystyle v_y(t)=- \mu gt.\) |
A hasáb gyorsulása negyed rezgés után csökken nullára:
| \(\displaystyle (10)\) | \(\displaystyle t_0=\dfrac{T}{4}=\dfrac{\pi}{2}\sqrt{\dfrac{M}{D}},\) |
ami (1) alapján így is írható:
\(\displaystyle t_0=\dfrac{\pi}{2}\sqrt{\dfrac{s}{g}}=0{,}2\ \rm s.\)
\(\displaystyle b)\) A csúszás akkor szűnik meg, amikor a két test sebessége megegyezik:
\(\displaystyle v_x(t_0)=v_y(t_0),\)
ahonnan (6), (7), (9) és (10) felhasználásával kapjuk, hogy
\(\displaystyle \ell=\dfrac{\mu gM}{D}\left(\dfrac{\pi}{2}+\dfrac{m}{M}\right).\)
Innen látszik, hogy a (2) feltétel biztosan teljesül, hiszen \(\displaystyle \pi/2>1\). Az \(\displaystyle m\) tömeg nagyságát nem ismerjük, de biztosan igaz, hogy \(\displaystyle m>0\), ennek megfelelően
\(\displaystyle \ell>\dfrac{\pi}{2}\cdot \dfrac{\mu M g}{D}=\dfrac{\pi}{2}\,\mu s=0{,}047\ {\rm m} \approx 5\ \rm cm.\)
\(\displaystyle c)\) A kockának a hasábhoz viszonyított elmozdulása (tehát a csúszásának hossza) \(\displaystyle t_0\) idő alatt
\(\displaystyle \Delta s=y(t_0)-x(t_0), \)
ami (5), (8) és (10) szerint
\(\displaystyle \Delta s=\mu s\left[\left(\dfrac{\pi}{2}+\dfrac{m}{M}\right)-\dfrac{\pi^2 }8\right] -\mu s\dfrac{m}{M}=\mu s \left( \dfrac{\pi}{2} -\dfrac{\pi^2 }8\right)\approx 1\ \rm cm.\)
(Érdekes, hogy \(\displaystyle \Delta s\) nem függ a kocka \(\displaystyle m\) tömegétől, emiatt nem okozott problémát, hogy annak nagysága nem szerepelt a megadott számadatok között.)
Megjegyzés. Belátható, hogy a csúszás megszűnte után, amikor a hasáb és a kocka egyetlen testként mozog, a kockára ható (vízszintes) erő nem haladja meg a \(\displaystyle \mu mg\) kritikus értéket, tehát a továbbiakban semmikor nem kezd újra csúszni.
A csúszás megszűntének pillanatában mind a hasáb, mind pedig a kocka gyorsulása ugrásszerűen megváltozik, a közös gyorsulásuk a tömegközéppont korábbi gyorsulásával egyezik meg.
Statisztika:
11 dolgozat érkezett. 6 pontot kapott: Bencz Benedek, Flóring Balázs, Molnár Kristóf, Szabó Zsombor. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2023. januári fizika feladatai