 |
A P. 5471. feladat (2023. február) |
P. 5471. Három egyforma, \(\displaystyle R\) sugarú, \(\displaystyle m\) tömegű jéghengert készítünk, és azokat az ábrán látható helyzetből kezdősebesség nélkül elengedjük. A jég felülete nagyon síkos, emiatt a súrlódás mindenhol elhanyagolható.
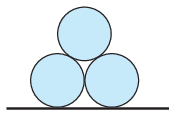
\(\displaystyle a)\) Határozzuk meg és ábrázoljuk vázlatosan az egyik alsó jéghenger mozgási energiáját a felső henger elmozdulásának függvényében!
\(\displaystyle b)\) Mekkora sebességgel csapódik a felső jéghenger a talajhoz, és mekkora sebességre gyorsul fel a másik két jéghenger?
Közli: Cserti József, Budapest
(6 pont)
A beküldési határidő 2023. március 16-án LEJÁRT.
Megoldás. Tekintsük azt a helyzetet, amikor az alsó két jéghenger tengelyének távolsága \(\displaystyle 2x\), a felső henger tengelye pedig \(\displaystyle R+y\) magasságban van (1. ábra). A jéghengerek sebessége \(\displaystyle \pm v_x\), illetve \(\displaystyle v_y\). Mivel a súrlódás elhanyagolható, a hengerek nem jönnek forgásba. Az indulás pillanatában
\(\displaystyle x=R;\qquad y=\sqrt3R\qquad\text{és}\qquad v_x=v_y=0.\)
1. ábra
A középső henger (függőleges) elmozdulása így írható:
| \(\displaystyle (1)\) | \(\displaystyle s=\sqrt3R-y.\) |
A felső és bármelyik alsó jéghenger távolsága állandó, vagyis fennáll az
\(\displaystyle \sqrt{x^2+y^2}=2R\)
kényszerfeltétel. Ez a távolság akkor marad időben állandó, ha a sebességek megfelelő komponensei megegyeznek:
\(\displaystyle v_y\sin\varphi\left(\equiv v_y \dfrac{y}{2R}\right)=v_x\cos\varphi\left(\equiv v_x\frac{x}{2R}\right),\)
tehát
| \(\displaystyle (2)\) | \(\displaystyle v_y=v_x\dfrac{x}{y}=v_x\dfrac{\sqrt{4R^2-y^2}}{y}.\) |
Az energiamegmaradás tétele szerint
\(\displaystyle 2\cdot \frac12mv_x^2+\frac12mv_y^2=mgs,\)
vagyis (1) és (2) felhasználásával az alsó hengerek valamelyikének mozgási energiája
\(\displaystyle E=\frac12mv_x^2=mgR \frac{\sqrt3-(y/R)}{ 1+4(R/y)^2}.\)
Vezessük be a \(\displaystyle \xi=\frac{y}{R}\) és az \(\displaystyle {\cal E}= \dfrac{E}{mgR} \) dimenziótlan változókat (az \(\displaystyle s\) elmozdulás \(\displaystyle (\sqrt3-\xi)R\) alakban fejezhető ki). Fejezzük ki, majd ábrázoljuk \(\displaystyle \cal E\)-t \(\displaystyle \xi\), illetve \(\displaystyle s\) függvényében (2. ábra).
\(\displaystyle {\cal E}=\xi^2\frac{\sqrt3-\xi}{4+\xi^2}.\)
2. ábra
Az ábrán látszik, hogy csökkenő \(\displaystyle \xi\) (vagyis növekvő \(\displaystyle s\)) mellett \(\displaystyle \cal E\)-nek \(\displaystyle \xi=\xi_0=1{,}056\)-nál lokális maximuma van, ennél kisebb \(\displaystyle \xi\) értékeknél \(\displaystyle \cal E\) (és ezzel arányosan az \(\displaystyle E\) mozgási energia) egyre kisebbnek adódik, amint azt a grafikonok piros ága mutatja. Ha ez valóban így történne, akkor a felső jéghenger lassítaná az alsó hengereket, vagyis az érintkezési pontoknál nem tolná, hanem visszafelé húzná azokat. Ez nyilván nem lehetséges, hanem a hengerek elválnak egymástól, és a két alsó henger szabadon mozogva megtartja a mozgási energiáját (lásd a grafikonok zöld ágát), és \(\displaystyle v_\text{x,max}\) sebességgel fognak mozogni még akkor is, amikor a középső henger a talajhoz csapódik. Ez a sebesség
\(\displaystyle v_\text{x,max}=\sqrt{\dfrac{2E_\text{max}}{m}}= \sqrt{\dfrac{2mgR{\cal E}_\text{max}}{m}}=0{,}54\sqrt{Rg}.\)
A függőlegesen lefelé mozgó henger maximális mozgási energiáját ugyancsak az energiamegmaradás törvényéből kaphatjuk meg:
\(\displaystyle \frac12mv_\text{y,max}^2=\sqrt3 mgR-2E_\text{max}= (\sqrt3-2\cdot 0{,}147)mgR,\)
ahonnan
\(\displaystyle v_\text{y,max}=1{,}69\sqrt{Rg}.\)
Statisztika:
13 dolgozat érkezett. 6 pontot kapott: Schmercz Blanka. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2023. februári fizika feladatai