 |
A P. 5477. feladat (2023. március) |
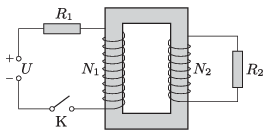
P. 5477. Egy U=24 V feszültségű ideális telepből, R1=500 Ω-os és R2=300 Ω-os ellenállásokból, egy kapcsolóból, valamint egy ideális transzformátorból az ábrán látható kapcsolást állítottuk össze. A transzformátor primer tekercsének menetszáma N1=800, a szekunder tekercsé N2=1000. A hosszú ideje nyitva lévő kapcsolót egyszer csak zárjuk. Mekkora áram folyik a primer és szekunder körben közvetlenül a kapcsoló zárása után?
Közli: Vigh Máté, Biatorbágy
(5 pont)
A beküldési határidő 2023. április 17-én LEJÁRT.
Megoldás. Legyen a vasmagban a mágneses fluxus Φ. (Ez a vasmag bármelyik keresztmetszeténél ugyanakkora, viszont időben változó mennyiség.) A hosszú ideje nyitott állású kapcsolónál a transzformátor egyik tekercsében sem folyik áram, így a fluxus nulla. Mivel hirtelen (,,pillanatszerűen'') nem változhat meg a fluxus, közvetlenül a kapcsoló zárása után is Φ=0.
Jelöljük a primer tekercs áramerősségét a kapcsoló zárását követő pillanatban I1-gyel, a szekunder tekercsét I2-vel. Az áramok által létrehozott mágneses fluxus a menetszámokkal arányos, így
| (1) | N1I1−N2I2=0. |
(A második tag előjele, az áram irányításától és a tekercselés irányától függően pozitív is lehet.)
A kapcsoló zárása után a vasmag mágneses fluxusa időben változni kezd, a változás üteme kezdetben
ΔΦΔt=U0.
A változó fluxus miatt a tekercsek minden menetében −U0 nagyságú feszültség indukálódik.
Írjuk fel a huroktörvényt a primer és a szekunder tekercs áramkörére:
| (2), | U−I1R1−N1U0=0, |
majd a szekunder körre is:
| (3) | I2R2−N2U0=0. |
Az (1)-(3) egyenletekből kiszámíthatjuk, hogy
I1=UN22N22R1+N21R2=35 mA,
I2=UN1N2N22R1+N21R2=28 mA,
továbbá megkapjuk a menetenként indukálódó feszültséget is:
U0=8,3 mV.
Statisztika:
13 dolgozat érkezett. 5 pontot kapott: Klement Tamás, Molnár Zétény. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 5 versenyző.
A KöMaL 2023. márciusi fizika feladatai
|
|

