 |
A P. 5480. feladat (2023. március) |
P. 5480. Egy függőleges sík adott \(\displaystyle P\) pontján keresztül különböző hajlásszögű (a síkra merőleges) lejtőket fektetünk, és ezeken kezdősebesség nélkül indítva pontszerűnek tekinthető testeket csúsztatunk le. Hol helyezkednek el azok a pontok, ahová a lecsúszó testek adott \(\displaystyle t\) idő alatt eljutnak? A súrlódási együttható a lejtők és a testek között \(\displaystyle \mu\).
Galileo Galilei (1564–1642) feladata nyomán
(6 pont)
A beküldési határidő 2023. április 17-én LEJÁRT.
I. megoldás. Válasszunk egy olyan koordináta-rendszert, amelynek origója a \(\displaystyle P\) pont, \(\displaystyle x\) tengelye vízszintes, \(\displaystyle y\) tengelye pedig függőlegesen felfelé mutat (1. ábra).
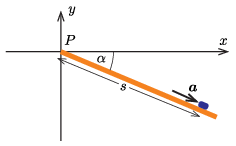
1. ábra
A súrlódva lecsúszó test gyorsulása az \(\displaystyle \arctg\mu<\alpha\le 90^\circ\) hajlásszögű lejtőn
| \(\displaystyle (1)\) | \(\displaystyle a(\alpha)=g(\sin\alpha-\mu\cos\alpha),\) |
így az adott \(\displaystyle t\) idő alatt
\(\displaystyle s(\alpha)=\frac{a(\alpha)}{2}t^2=\frac{g}{2}t^2(\sin\alpha-\mu\cos\alpha)\)
utat tesz meg. Érdemes bevezetni a \(\displaystyle h=gt^2/2\) jelölést (\(\displaystyle h\) az a távolság, amennyit a szabadon eső test \(\displaystyle t\) idő alatt megtesz), ezzel a test koordinátái
| \(\displaystyle (2)\) | \(\displaystyle x(\alpha)=h(\sin\alpha-\mu\cos\alpha)\cos\alpha,\) |
| \(\displaystyle (3)\) | \(\displaystyle y(\alpha)=-h(\sin\alpha-\mu\cos\alpha)\sin\alpha.\) |
A (2) és (3) összefüggések a keresett pontokat leíró görbe paraméteres egyenletei, amelyekből \(\displaystyle \alpha\) kiküszöbölése után megkaphatjuk a keresett mértani hely egyenletét \(\displaystyle y=f(x)\) vagy \(\displaystyle F(x,y)=0\) alakban. Felhasználva a
\(\displaystyle \sin\alpha\,\cos\alpha=\frac{\sin 2\alpha}{2},\qquad \cos^2\alpha=\frac{1+\cos 2\alpha}{2},\qquad \sin^2\alpha=\frac{1-\cos 2\alpha}{2}\)
trigonometrikus azonosságokat, (2) és (3) így írható át:
| \(\displaystyle (4)\) | \(\displaystyle x+\frac{\mu h}{2 }=\frac{h}{2}\left(\sin 2\alpha-\mu \cos 2\alpha\right),\) |
| \(\displaystyle (4)\) | \(\displaystyle y+\frac{h}{2}=\frac{h}{2}\left(\mu\sin 2\alpha+\cos 2\alpha\right).\) |
Most már könnyen kiküszöbölhetjük az \(\displaystyle \alpha\) paramétert, ha a (3) és (4) egyenleteket négyzetre emeljük és összeadjuk:
\(\displaystyle \left( x+\frac{\mu h}{2 }\right)^2+ \left( y+\frac{h}{2}\right)^2=\frac{h^2}4(1+\mu^2).\)

2. ábra
Ez egy olyan kör egyenlete, amelynek sugara
\(\displaystyle R=\frac{h}{2}\sqrt{1+\mu^2},\)
középpontjának koordinátái pedig
\(\displaystyle x_0=-\frac{\mu h}{2 }; \qquad y_0=-\frac{ h}{2 }.\)
Mivel a fenti számolás csak a \(\displaystyle 90^\circ\ge \alpha>\arctg \mu\) hajlásszögű lejtőkre érvényes, a kérdéses pontok a 2. ábrán látható körnek csak a zölden jelölt részén helyezkednek el. Amennyiben \(\displaystyle \alpha<-\arctg \mu\) (vagyis a \(\displaystyle P\) ponttól induló lejtő bal felé lejt), a kérdéses pontok a zöld körívnek az \(\displaystyle y\) tengelyre vett tükörképén helyezkednek el. Ha pedig
\(\displaystyle \vert\alpha\vert\le\arctg \mu,\)
a test el se indul a lejtőn, folyamatosan (tehát \(\displaystyle t\) idő elteltével is) a \(\displaystyle P\) pontban marad.
II. megoldás. Egy \(\displaystyle \alpha\) hajlásszögű, \(\displaystyle \mu\) súrlódási együtthatóval jellemezhető lejtőre helyezett test akkor indul el (akkor tud gyorsulni), ha
\(\displaystyle \tg\alpha > \mu,\)
vagyis ha
\(\displaystyle \alpha >\arctg\mu\equiv\varepsilon.\)
Az \(\displaystyle \varepsilon\) szöget – érthető okokból – súrlódási határszögnek nevezik.
Az \(\displaystyle \alpha\) hajlásszögű lejtőn mozgó test gyorsulása
\(\displaystyle a=g(\sin\alpha-\tg \varepsilon \cos\alpha)= \frac{g}{\cos\varepsilon}(\sin\alpha\cos\varepsilon-\cos\alpha\sin\varepsilon)=\frac{g}{\cos\varepsilon}\sin(\alpha-\varepsilon).\)
Ez az összefüggés azt mutatja, hogy a súrlódásos lejtőn csúszó test mozgása éppen olyan, mintha \(\displaystyle g'=\cfrac{g}{\cos\varepsilon}\) nehézségi gyorsulás mellett egy súrlódásmentes lejtőn mozogna a test, amelynek hajlásszöge \(\displaystyle \varepsilon\)-nal kisebb, mint a tényleges \(\displaystyle \alpha\) hajlásszög. Ez utóbbi szögeltérést úgy is értelmezhetjük, hogy a \(\displaystyle \boldsymbol g'\) nehézségi gyorsulás nem függőlegesen lefelé mutató, hanem a függőlegessel \(\displaystyle \varepsilon\) szöget bezáró, a lejtő síkjának normálvektorához közelebb álló vektor (3. ábra).

3. ábra
Már Galilei is felismerte, hogy a \(\displaystyle P\) pontból különböző meredekségű, súrlódásmentes lejtőkön lecsúszó testek adott \(\displaystyle t\) idő alatt egy olyan kör pontjaiba jutnak el, amely kör illeszkedik a \(\displaystyle P\) pontra és a síkja függőleges. (Ma már – a Newton-törvényeket ismerve – azt is tudjuk, hogy a kör átmérője \(\displaystyle h'=g't^2/2\).)
Alkalmazzuk ezt a felismerést a súrlódó lejtő esetére.

4. ábra
A test \(\displaystyle t\) idő alatt
\(\displaystyle s=\dfrac{g't^2}{2}\sin(\alpha-\varepsilon)= \cfrac{h}{\cos\varepsilon}\sin(\alpha-\varepsilon)\)
utat tesz meg, és így a \(\displaystyle \boldsymbol g'\) irányú, \(\displaystyle h'\) átmérőjű Thalesz-kör zölden jelölt részének pontjaiba kerülhet (4. ábra). A kör középpontja a \(\displaystyle P\) pont alatt \(\displaystyle h/2\) mélységben és a \(\displaystyle P\)-n átmenő függőleges egyenestől
\(\displaystyle \frac{h'}{2}\sin \varepsilon=\frac {h}{2\cos\varepsilon}\sin\varepsilon=\frac{h}{2}\tg\varepsilon=\frac{h}{2}\mu\)
távolságra található, összhangban az I. megoldás eredményével.

Statisztika:
14 dolgozat érkezett. 6 pontot kapott: Bencz Benedek, Fehérvári Donát, Halász Henrik, Richlik Márton, Schmercz Blanka, Tárnok Ede . 4 pontot kapott: 4 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2023. márciusi fizika feladatai

