 |
A P. 5500. feladat (2023. szeptember) |
P. 5500. Egy hinta hosszú kötelei álló helyzetben legfeljebb \(\displaystyle M\) tömegű terhet bírnak el biztonságosan. Legfeljebb mekkora tömegű ember hintázhat rajta, ha a maximális kitérés egy \(\displaystyle \alpha\) hegyesszög? Eredményünket ábrázoljuk grafikonon!
Közli: Rakovszky Andorás, Budapest
(4 pont)
A beküldési határidő 2023. október 16-án LEJÁRT.
Megoldás. Legyen a (kötél hosszához képest pontszerűnek tekintett) hintázó ember tömege \(\displaystyle m\), a kötelek hossza \(\displaystyle \ell\), a teherbírásásuk pedig \(\displaystyle Mg\). Ha a maximális kitérés \(\displaystyle \alpha\), akkor a test sebessége \(\displaystyle \varphi\) szögkitérésű helyzetben az energiamegmaradás tétele szerint
| \(\displaystyle (1)\) | \(\displaystyle v(\varphi)=\sqrt{2g\ell(\cos\varphi-\cos\alpha)}.\) |
A test centripetális gyorsulását ebben a helyzetben az \(\displaystyle F\) fonálerő és a nehézségi erő fonálirányú komponense biztosítja. Newton mozgástörvénye szerint
\(\displaystyle \frac{m\,v(\varphi)^2}{\ell}=F-mg\cos\varphi,\)
ahonnan (1) felhasználásával
\(\displaystyle F=mg(3\cos\varphi-2\cos\alpha).\)
Ez az erő (adott \(\displaystyle \alpha\) mellett) \(\displaystyle \varphi=0\)-nál a legnagyobb:
\(\displaystyle F_\text{max}(\alpha)=mg(3-2\cos\alpha)\le Mg.\)
Innen következik, hogy
\(\displaystyle m\le m_\text{max}=\frac{M}{3-2\cos\alpha}.\)
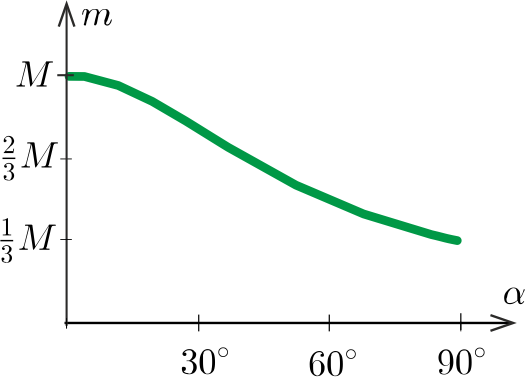
A hintázó ember tömege tehát az ábrán látható zöld görbe alatti tartományba eshet.
Statisztika:
76 dolgozat érkezett. 4 pontot kapott: Alexandrova Angelina, Bánkuti Bálint, Barna Márton, Beke Botond, Bélteki Teó, Benes András, Bocor Gergely, Bunford Luca, Csapó András, Csiszár András, Csóka Péter, Dancsák Dénes, Daniils Koselevs, Dobos Anita, Elekes Dorottya, Fajszi Karsa, Farkas 145 László, Flóring Balázs, Hegedüs Márk, Hornok Máté, Hüvös Gergely, Kiss 131 Adorján Timon, Magyar Zsófia, Masa Barnabás, Molnár Kristóf, Molnár Zétény, Seprődi Barnabás Bendegúz, Szabó Donát, Tóth Hanga Katalin, Vincze Farkas Csongor. 3 pontot kapott: Balogh Áron , Boér Panna Rita, Czirják Márton Pál, Erős Fanni, Fehérvári Donát, Halász Sámuel, Harkai Barnabás, Képes Botond, Muraközi Péter, Sütő Áron, Tibor Varga, Zhang Wenshuo Steve. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 11 versenyző. 0 pontot kapott: 6 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2023. szeptemberi fizika feladatai