A P. 5507. feladat (2023. szeptember)

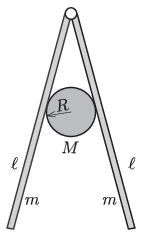
P. 5507. Két egyforma, érdes deszkát súrlódásmentes, vízszintes helyzetben rögzített tengely kapcsol össze. Mindkét deszka tömege $\displaystyle m$, hossza $\displaystyle \ell$.

A deszkák közé egy $\displaystyle M=\frac 12 m$ tömegű, $\displaystyle R=\frac 15 \ell$ sugarú hengert helyezünk.

$\displaystyle a)$ Legalább mekkora kell legyen a deszkák és a henger közötti tapadási súrlódás együtthatója, hogy a henger valahol (egy alkalmasan választott helyen) egyensúlyban maradhasson?

$\displaystyle b)$ Mekkora lehet a deszkák által bezárt szög a henger egyensúlyi állapotában?

Dózsa Márton (1914–1999) feladata nyomán

(6 pont)

A beküldési határidő 2023. október 16-án LEJÁRT.

Megoldás. Legyen a deszkák által bezárt szög $\displaystyle 2\varphi$, az egyes deszkák és a henger között ható nyomóerő $\displaystyle N$, a súrlódási erő pedig $\displaystyle S$ (lásd az 1. ábrát).

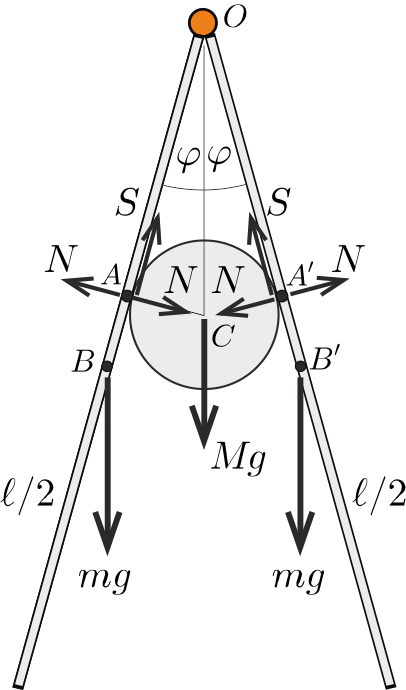
1. ábra

Mivel a deszkák és a henger érintkezési pontjai a forgástengelytől

$\displaystyle OA=OA'=\frac{R}{\tg\varphi}=\frac{\ell}{5}\cdot \frac{\cos\varphi}{\sin\varphi}$

távol vannak, továbbá $\displaystyle OB=OB'=\ell/2$, a deszkáknak az $\displaystyle O$ tengelyre vonatkoztatott forgatónyomaték-egyensúlyi feltétele:

$\displaystyle N\,\frac{\ell}{5}\cdot \frac{\cos\varphi}{\sin\varphi}=mg\,\cfrac{\ell}{2}\sin\varphi,$

vagyis

Teljesülnie kell még a hengerre ható erők egyensúlyi feltételének is. Az eredő erő vízszintes komponense a szimmetria miatt biztosan nulla, így elegendő a függőleges erőkomponenseket összegezni:

$\displaystyle Mg+2N\sin\varphi-2S\cos\varphi=0,$

ahonnan $\displaystyle M=m/2$ és (1) felhasználásával

adódik.

A tapadó súrlódás feltétele: $\displaystyle S\le \mu N$, vagyis (1) és (2) ismeretében

$\displaystyle \mu \ge \frac{S}{N}\equiv\tg\varphi+\frac{1}{10\,\tg^2\varphi}+\frac{1}{10}.$

Ábrázolva az $\displaystyle S/N$ hányadost $\displaystyle \varphi$ függvényében a 2. ábrán látható görbét kapjuk.

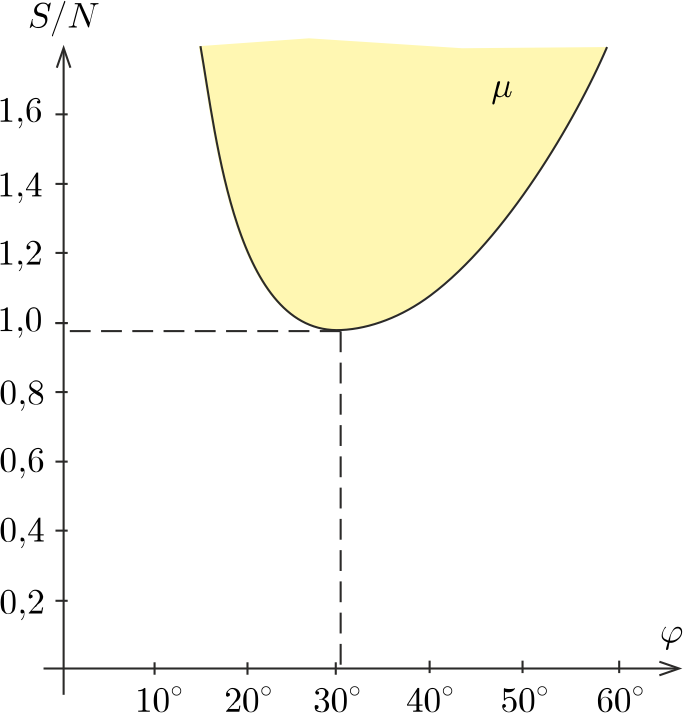
2. ábra

A tapadó súrlódás akkor tarthat egyensúlyt, ha $\displaystyle \mu$ a sárga tartományba esik. Láthatjuk, hogy a

$\displaystyle \mu\ge \mu_\text{min}\approx 1{,}0$

feltételnek kell teljesülnie, és a legkisebb súrlódási együttható esetén csak a $\displaystyle 2\varphi\approx 60^\circ$ szöget bezáró deszkák lehetnek egyensúlyban. Ha $\displaystyle \mu$-t valahogyan meg tudjuk növelni (pl. a deszkák felületét érdesebbé tesszük), akkor egyre szélesebb szögtartományban alakulhat ki egyensúly.

Ezeket az eredményeket más úton (grafikus ábrázolás vagy differenciálszámítás nélkül) is megkaphatjuk. Bevezetve az $\displaystyle x\equiv\tg\varphi$ jelölést az egyensúly feltétele:

$\displaystyle \mu \ge x+\frac{1}{10\,x^2}+\frac{1}{10}\equiv f(x).$

Alkalmazva a számtani és mértani közepekre vonatkozó egyenlőtlenséget:

$\displaystyle f(x)-\frac1{10}=\frac{x}{2}+\frac{x}{2}+\frac{1}{10\,x^2}\ge 3\sqrt[3]{\frac{x}{2}\cdot\frac{x}{2}\cdot\frac{1}{10\,x^2}}= \sqrt[3]{\frac{27}{40}}.$

$\displaystyle f(x)$ legkisebb értékénél fennáll:

$\displaystyle \frac{x_0}{2}=\frac{1}{10\,x_0^2}, \qquad \text{vagyis}\qquad x_0=\frac{1}{\root 3 \of {5}}\qquad\text{és}\qquad \varphi_0=\arctg x_0=30{,}3^\circ.$

A legkisebb súrlódási együttható:

$\displaystyle \mu_\text{min}=f(x_0)=\sqrt[3]{\frac{27}{40}}+\frac1{10}=0{,}977\approx 1{,}0.$

Megjegyzés. A deszkák és a henger érintkezési pontjai legfeljebb $\displaystyle \ell$ távolságra lehetnek a tengelytől. Emiatt teljesülnie kell még a

$\displaystyle \tg\varphi \ge \frac{R}{\ell}=\frac15,\qquad \text{vagyis}\qquad \varphi\ge 11{,}3^\circ$

feltételnek is.

Statisztika:

47 dolgozat érkezett.
6 pontot kapott:	Alexandrova Angelina, Bencz Benedek, Csapó András, Csóka Péter, Daniils Koselevs, Debreceni Dániel, Fehérvári Donát, Hegedüs Márk, Hüvös Gergely, Képes Botond, Kiss 131 Adorján Timon, Kovács Kristóf , Lincoln Liu, Molnár Kristóf, Seprődi Barnabás Bendegúz, Szabó Donát, Tárnok Ede , Tóth Kolos Barnabás, Vidor Nikoletta, Vincze Farkas Csongor.
5 pontot kapott:	Beke Botond, Czirják Márton Pál, Diaconescu Tashi, Simon János Dániel, Žigo Boglárka.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2023. szeptemberi fizika feladatai