A P. 5511. feladat (2023. október)

P. 5511. Egy elhanyagolható tömegű, \(\displaystyle R\) sugarú abroncs egyik átmérőjének két végpontjába egy \(\displaystyle m\), illetve egy \(\displaystyle M=2m\) tömegű, pontszerű nehezéket erősítettünk. A függőleges síkú abroncsot asztallapra helyezzük úgy, hogy kezdetben a két nehezék azonos függőleges egyenesen helyezkedik el (a nehezebb van felül). Az abroncsot ebből az instabil egyensúlyi állapotból elengedjük. Az abroncs és az asztallap közötti súrlódás elegendően nagy ahhoz, hogy az abroncs csúszásmentesen gördüljön az asztallapon.

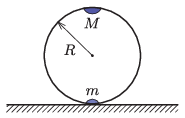
\(\displaystyle a)\) Mekkora az abroncs középpontjának sebessége, amikor az \(\displaystyle M\) tömegű nehezék eléri pályájának legalsó pontját?

\(\displaystyle b)\) Mekkora az \(\displaystyle a)\) esetben az asztalra ható nyomóerő?

Közli: Vigh Máté, Biatorbágy

(5 pont)

A beküldési határidő 2023. november 15-én LEJÁRT.

Megoldás. \(\displaystyle a)\) A kérdéses pillanatban legyen az abroncs középpontjának sebessége \(\displaystyle v\). A csúszásmentesen gördülő abroncs szögsebessége ekkor \(\displaystyle \omega=v/R\), a felülre került \(\displaystyle m\) tömegű test sebessége pedig \(\displaystyle 2v\).

A rendszer mozgási energiája a kérdéses helyzetben (mivel ebben a helyzetben csak az \(\displaystyle m\) tömegű test mozog)

\(\displaystyle E_\text{m}=\frac12 m (2v)^2=2mv^2.\)

Az energiamegmaradás törvénye szerint

\(\displaystyle 2RMg= 2mv^2+2Rmg,\)

vagyis az abroncs középpontjának sebessége:

\(\displaystyle v=\sqrt{gR\left(\frac{M}{m}-1\right)}=\sqrt{gR}.\)

\(\displaystyle b)\) Az \(\displaystyle M\) tömegű test legmélyebb helyzeténél az abroncs középpontja éppen nem gyorsul. Az \(\displaystyle m\) tömegű test gyorsulása így \(\displaystyle R\omega^2\) lefelé, az \(\displaystyle M\) tömegű test gyorsulása pedig \(\displaystyle R\omega^2\) felfelé. Ha az asztal által az abroncsra kifejtett erő \(\displaystyle F\) (ugyanekkora nagyságú az asztalra ható nyomóerő is), akkor az egész rendszerre felírt Newton-egyenlet szerint

\(\displaystyle Mg+mg-F=mR\omega^2-MR\omega^2,\)

ahonnan \(\displaystyle \omega\) és \(\displaystyle v\) ismert kifejezésének behelyettesítése után kapjuk, hogy

\(\displaystyle F=(M+m)g+(M-m)g=2Mg=4mg.\)

Statisztika:

55 dolgozat érkezett.
5 pontot kapott:	Csapó András, Czirják Márton Pál, Fehérvári Donát, Flóring Balázs, Hornok Máté, Képes Botond, Kis Márton Tamás, Kiss 131 Adorján Timon, Klement Tamás, Papp András, Simon János Dániel, Tóth Kolos Barnabás, Vágó Botond, Zádori Gellért, Zólomy Csanád Zsolt.
4 pontot kapott:	Seprődi Barnabás Bendegúz.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	11 versenyző.
0 pontot kapott:	14 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2023. októberi fizika feladatai