 |
A P. 5514. feladat (2023. október) |
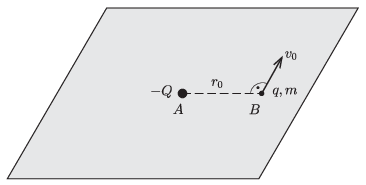
P. 5514. Vízszintes, sík felület egyik, \(\displaystyle A\) pontjában egy pontszerűnek tekinthető, \(\displaystyle -Q<0\) töltésű test van rögzítve. A síkon egy szintén pontszerűnek tekinthető, \(\displaystyle m\) tömegű, \(\displaystyle q>0\) töltésű test súrlódásmentesen tud mozogni. Kezdetben az \(\displaystyle m\) tömegű test a \(\displaystyle B\) pontban van, ekkor a töltések távolsága \(\displaystyle r_0\), és az \(\displaystyle m\) tömegű testnek az \(\displaystyle AB\) szakaszra merőlegesen, a síkkal párhuzamosan \(\displaystyle v_0=\sqrt{\frac{kqQ}{mr_0}}\) nagyságú sebessége van.
(A mozgás közben a töltések nagysága nem változik.)
\(\displaystyle a)\) A mozgó test mennyi idő múlva jut ismét az \(\displaystyle AB\) pontok által meghatározott egyenesre?
\(\displaystyle b)\) Most a mozgó test kezdősebességének nagyságát felére csökkentjük. Az előbbi esetbeli időnek hányszorosa a kiindulási helytől a legtávolabbi helyig való legkorábbi eljutás ideje?
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2023. november 15-én LEJÁRT.
Megoldás. Vízszintes síkon súrlódásmentesen mozog a \(\displaystyle q\) töltés, vagyis a földi súlyerővel a megoldás során nem kell törődnünk. Mivel a töltések közti elektrosztatikus vonzóerő helyfüggése megegyezik a gravitációéval, a mozgás leírására használhatjuk a Kepler-törvényeket: a mozgó töltés ellipszis- vagy körpályán fog keringeni a rögzített töltés körül (lásd az ábrát).

\(\displaystyle a)\) Amikor a töltött test \(\displaystyle v_0\) sebességgel \(\displaystyle r_0\) sugarú körpályán mozog, akkor:
\(\displaystyle \frac{mv_0^2}{r_0}=k\frac{qQ}{r_0^2},\qquad\textrm{ vagyis} \qquad v_0=\sqrt{\frac{kqQ}{mr_0}}.\)
A feladatban éppen ekkora, a testeket összekötő egyenesre (vezérsugárra) merőleges kezdeti sebességet adtak meg, tehát éppen a körpálya valósul meg. A pálya az \(\displaystyle AB\) egyenest egy félkörív megtétele után a \(\displaystyle C\) pontban \(\displaystyle t_a=\pi r_0/v_0\) idő múlva éri el.
\(\displaystyle b)\) Ettől kisebb kezdősebesség esetén a pálya ellipszis lesz. A pálya és az \(\displaystyle AB\) egyenes metszéspontjai (\(\displaystyle B\) és \(\displaystyle D\)) a pálya aphélium (naptávol) és perihélium (napközel) pontjai. A sebesség csak ebben a két pontban merőleges a vezérsugárra. Az első pontban a test távolsága és sebessége \(\displaystyle r_1=r_0\), \(\displaystyle v_1=\frac{1}{2}v_0\), a másodikban \(\displaystyle r_2\), \(\displaystyle v_2\). A kérdezett időarány a fél keringési idők aránya, amit Kepler III. törvényéből tudnánk kiszámolni, ha ismernénk az ellipszispálya nagytengelyének hosszát. Meg kell tehát határoznunk \(\displaystyle r_2\)-t.
Az ismeretlen \(\displaystyle r_2\) és \(\displaystyle v_2\) mennyiségekre két megmaradási törvényt tudunk felírni. A perdületmegmaradást:
\(\displaystyle m v_1 r_1=m v_2 r_2,\)
ami ebben az alakban csak \(\displaystyle B\)-ben és \(\displaystyle D\)-ben érvényes; valamint az energiamegmaradást:
\(\displaystyle \frac{1}{2}mv_1^2-\frac{kqQ}{r_1}=\frac{1}{2}mv_2^2-\frac{kqQ}{r_2},\)
ami a pálya mentén végig teljesül. Rendezzük át az utóbbi egyenletet, és használjuk a töltések és a tömeg helyett inkább a körpálya \(\displaystyle r_0\) és \(\displaystyle v_0\) paramétereit:
\(\displaystyle 2v_0^2 r_0 \bigg(\frac{1}{r_2}-\frac{1}{r_1}\bigg) = v_2^2 - v_1^2.\)
Helyettesítsük be a perdületmegmaradást kifejező \(\displaystyle \displaystyle v_2=\frac{v_1r_1}{r_2}\)-t:
\(\displaystyle 2v_0^2\frac{r_0}{r_1}\bigg(\frac{r_1}{r_2}-1\bigg) = v_1^2\Bigg(\bigg(\frac{r_1}{r_2}\bigg)^2 -1\Bigg).\)
Az egyenletnek könnyen megtalálható, de semmitmondó (triviális) gyöke az \(\displaystyle r_2=r_1\), ami magának a \(\displaystyle B\) pontnak a távolsága. Minket a másik \(\displaystyle r_2\ne r_1\) gyök érdekel, ezért eloszthatjuk az egyenletet \(\displaystyle \displaystyle \bigg(\frac{r_1}{r_2}-1\bigg)\)-gyel:
\(\displaystyle 2v_0^2\frac{r_0}{r_1} = v_1^2\bigg(\frac{r_1}{r_2}+1\bigg).\)
Helyettesítsük be a megadott \(\displaystyle r_1=r_0\) és \(\displaystyle v_1=\frac{1}{2}v_0\) kezdeti értékeket!
\(\displaystyle 2v_0^2 = \bigg(\frac{v_0}{2}\bigg)^2\bigg(\frac{r_1}{r_2}+1\bigg),\)
amiből az \(\displaystyle AD\) távolság: \(\displaystyle r_2=\frac{1}{7}r_0\). Az ellipszis és a körpálya nagytengelyeinek aránya tehát
\(\displaystyle \frac{1+\frac{1}{7}}{2} = \frac{4}{7},\)
a (fél) keringési időké pedig Kepler III. törvénye szerint
\(\displaystyle \bigg(\frac{4}{7}\bigg)^{3/2}\approx 0{,}43.\)
Statisztika:
32 dolgozat érkezett. 5 pontot kapott: Bélteki Teó, Bencz Benedek, Csiszár András, Csóka Péter, Dobos Anita, Hüvös Gergely, Kis Márton Tamás, Kiss 131 Adorján Timon, Klement Tamás, Magyar Zsófia, Szabó Donát, Tárnok Ede . 4 pontot kapott: Barna Márton, Csapó András, Fajszi Karsa, Masa Barnabás, Tóth Kolos Barnabás, Vágó Botond, Vincze Farkas Csongor. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 3 versenyző.
A KöMaL 2023. októberi fizika feladatai

