A P. 5519. feladat (2023. november)

P. 5519. Dionüszosz vízszintes talajon elhelyezett egymás tetején $\displaystyle 2$ egyforma, $\displaystyle h$ magasságú, egyenes henger alakú, borral közel teletöltött hordót. Héraklész tizenharmadik próbájaként azt a feladatot kapja, hogy fúrjon a hordók falára merőlegesen egy-egy lyukat az alsó, illetve a felső hordóba, az adott hordó aljától mért ugyanakkora $\displaystyle xh$ magasságban.

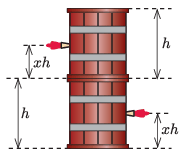
Hogyan válassza meg Héraklész a dimenziótlan $\displaystyle x$ arányszám értékét, hogy a borsugarak földet érési pontjai a lehető legmesszebb kerüljenek egymástól?

Dürer-verseny feladata nyomán

(5 pont)

A beküldési határidő 2023. december 15-én LEJÁRT.

Megoldás. Mindkét hordónál a lyuk és a hordó teteje között $\displaystyle h-xh=h(1-x)$ a szintkülönbség, így mindkét borsugár kiáramlási sebessége a Torricelli-törvény szerint

$\displaystyle v=\sqrt{2gh(1-x)}.$

Amennyiben a lyuk $\displaystyle H$ magasan van a talaj felett, a borsugár egyes (tömegpontoknak tekinthető) darabkáinak esési ideje

$\displaystyle T=\sqrt{\frac{2H}{g}},$

így a borsugár a hordótól

$\displaystyle s=vT=2\sqrt{Hh(1-x)}$

távolságra csapódik a talajhoz. Az alsó hordónál $\displaystyle H=xh$, tehát

$\displaystyle s_1(x)=2h\sqrt{x(1-x)},$

a felső hordónál pedig $\displaystyle H=h+xh,$ így a hordótól való eltávolodása

$\displaystyle s_2(x)=2h\sqrt{(1+x)(1-x)}.$

A két becsapódási pont távolsága

$\displaystyle \ell =s_1(x)+d+s_2(x)=d+2h\left(\sqrt{x(1-x)}+\sqrt{1-x^2}\right),$

ahol $\displaystyle d$ a hordók átmérője, hiszen a maximális távolsághoz az is kell, hogy a lyukak a hordók átellenes oldalán legyenek. Mivel $\displaystyle h$ és $\displaystyle d$ ($\displaystyle x$-től független) állandók, Héraklész feladata az

$\displaystyle f(x)=\sqrt{x(1-x)}+\sqrt{1-x^2}$

függvény $\displaystyle 0<x< 1$ intervallumon felvett legnagyobb értékének, vagyis a maximumának megtalálása.

Erre hatféle módszert (!) is javasolhatunk neki. Az első egy grafikus közelítő módszer, a második felsőbb matematikát (differenciálszámítást) alkalmaz. Vannak még közelítésmentes, elemi megoldások is. A harmadik algebrai megoldás, a számtani-, a mértani- és a négyzetes közepekre vonatkozó egyenlőtlenségeket alkalmazza. A negyedik megoldási módszer lényege az $\displaystyle f(x)$ két tagja között fennálló ,,átskálázhatósági tulajdonság'' felismerése. Ennek az eljárásnak az az érdekessége, hogy bár $\displaystyle f(x)$ növekedési ütemére hivatkozik, de annak nagyságát (a többi módszertől eltérően) nem szükséges kiszámítanunk. Az ötödik (geometriai) módszer $\displaystyle f(x)$ növekedési (és csökkenési) ütemét vizsgálja, de nem igényli a differenciálszámítás ismeretét. Végül a hatodik megoldási mód körök egymásba transzformálhatóságát használja.

1. módszer. Valamilyen rajzolóprogram segítségével ábrázoljuk $\displaystyle f(x)$-et. A grafikonról (1. ábra) leolvashatjuk, hogy a függvény a maximumát $\displaystyle x\approx 0{,}33\approx \tfrac13$ értéknél veszi fel.

1. ábra

2. módszer. Az $\displaystyle f(x)$ függvény maximumánál teljesül, hogy

$\displaystyle f'(x)\equiv \frac{1-2x}{2\sqrt{x(1-x)}}- \frac{2x}{2\sqrt{1-x^2}} =0,$

ahonnan

$\displaystyle (1-2x)^2(1-x)(1+x)=4x^3(1-x) .$

Mivel $\displaystyle x<1$ (vagyis $\displaystyle x\ne 1)$, egyszerűsíthetünk $\displaystyle (1-x)$-szel:

$\displaystyle (1-2x)^2(1+x)=4x^3,$

azaz

$\displaystyle (1-4x+4x^2)+(x-4x^2+4x^3)=4x^3,$

vagyis

$\displaystyle 1-3x=0,$

tehát a maximum helye

$\displaystyle x_0=\frac13.$

Behelyettesítéssel kapjuk, hogy

$\displaystyle f_\text{max}=f(x_0)=\sqrt{\frac{2}{9}}+\sqrt{\frac{8}{9}}=\sqrt2,$

és így

$\displaystyle \ell_\text{max}=d+2\sqrt2 h.$

Héraklésznek tehát a hordókat az alsó harmadrészüknél kell megfúrnia, egymással ellentétes oldalon, hogy teljesítse a próbát.

3. módszer. Bontsuk fel $\displaystyle f(x)$-et két tényező szorzatára:

$\displaystyle f(x)=\sqrt{1-x}\cdot\left(\sqrt{x}+\sqrt{1+x}\right),$

és keressünk felső korlátot a második tényezőre. Kínálja magát az ötlet, hogy a számtani közép és a négyzetes közép közötti

$\displaystyle \frac{a+b}{2}\le \sqrt{\frac{a^2+b^2}{2}}$

egyenlőtlenséget alkalmazzuk, hiszen ekkor a négyzetgyökök négyzete két összevonható, lineáris kifejezés lesz. Az egyenlőség csak akkor áll fenn, ha $\displaystyle a=b$.

Esetünkben $\displaystyle a=\sqrt{x}$ és $\displaystyle b=\sqrt{1+x}$, ezek minden $\displaystyle x$-re különbözőek, az egyenlőtlenség tehát nem lehet ,,éles''.

$\displaystyle \sqrt{x}+\sqrt{1+x}<2\sqrt{\cfrac{x+(1+x)}{2} }=2\sqrt{x+\tfrac12}.$

Visszatérve $\displaystyle f(x)$ felső korlátjának kereséséhez:

$\displaystyle f(x)<2\sqrt{(1-x)\left(x+\tfrac12\right)}.$

Itt most a mértani és a számtani közepekre vonatkozó

$\displaystyle \sqrt{ab}\le \frac{a+b}{2}$

egyenlőtlenséget alkalmazhatjuk:

$\displaystyle f(x)<\frac{3}{2}.$

Ez egy igaz állítás, de nem adja meg $\displaystyle f(x)$ legnagyobb értékét, hiszen semmilyen $\displaystyle x$-nél nem éri el $\displaystyle f(x)$ a $\displaystyle \frac{3}{2}$ értéket.

Próbálkozhatunk azzal, hogy $\displaystyle \sqrt{1+x}$-et két egyenlő kifejezés összegére bontjuk:

$\displaystyle \sqrt{1+x}=\sqrt{\tfrac14(1+x)}+\sqrt{\tfrac14(1+x)},$

és három tagra írjuk fel a számtani és a négyzetes közepek

$\displaystyle \frac{a+b+c}{3}\le \sqrt{\frac{a^2+b^2+c^2}{3}}$

egyenlőtlenségét. (Az egynlőség $\displaystyle a=b=c$ esetén teljesül.) Jelen esetben

$\displaystyle \sqrt{x}+\sqrt{\tfrac14(1+x)}+\sqrt{\tfrac14(1+x)} \le \sqrt{3\left(x+\frac{1+x}{2} \right)}=\frac{3}{\sqrt2}\sqrt{x+\frac{1}{3}}.$

Az egyenlőség

$\displaystyle x=\frac{1+x}{4},\qquad\text{vagyis}\qquad x=\frac13$

esetén teljesül.

A teljes $\displaystyle f(x)$-re ezt írhatjuk fel:

$\displaystyle f(x)\equiv \sqrt{1-x}\left(\sqrt{x}+\sqrt{1+x}\right)\le \frac{3}{\sqrt2}\sqrt{1-x}\sqrt{x+\frac{1}{3}}\le \frac{3}{\sqrt2}\frac{1-x+x+\tfrac13}{2}=\sqrt{2}.$

Ez az egyenlőtlenság $\displaystyle 1-x=x+\tfrac13$, azaz $\displaystyle x=\tfrac13$-nál válik élessé, tehát ugyanott, ahol a korábbi (a négyzetes középre vonatkozó). Emiatt állíthatjuk, hogy

$\displaystyle f(x)\le \sqrt2,$

és az egyenlőség $\displaystyle x=\frac13$-nál teljesül, vagyis itt veszi fel $\displaystyle f(x)$ a maximélis értékét.

4. módszer. Vegyük észre, hogy az

$\displaystyle f(x)=u(x)+v(x)= \sqrt{x(1-x)}+\sqrt{(1 + x)(1-x)}$

kifejezés két tagja lényegében azonos szerkezetű, így megfelelő ,,skálatranszformációval'' azonos alakra hozható. Ha

$\displaystyle u(x)=\sqrt{x(1-x)},$

akkor

$\displaystyle v(x)=\sqrt{(1+x)(1-x)}=2\, u(y), \qquad \text{ahol}\qquad y=\frac{1-x}{2}.$

Valóban:

$\displaystyle 2u(y)=2\,\sqrt{y(1-y)}=2\sqrt{\left(\frac{1-x}{2}\right)\left(1-\frac{1-x}{2}\right)}=\sqrt{(1+x)(1-x)}=v(x).$

Ebből következően, ha az $\displaystyle u(x)$ érintőjének a meredeksége egy $\displaystyle x$ pontban $\displaystyle m(x)$, tehát a függvény értéke az $\displaystyle x+\Delta x$ pontban jó közelítéssel

$\displaystyle u(x+\Delta x)\cong u(x)+m(x)\Delta x,$

akkor

$\displaystyle v(x+\Delta x)=2u\left(\frac{1-x-\Delta x}{2} \right)\cong 2 u\left(\frac {1-x}2 \right)-2\,m\left(\frac {1-x}2 \right)\frac{\Delta x}{2},$

és így

$\displaystyle f(x+\Delta x)=u(x+\Delta x)+v(x+\Delta x)\cong f(x)+ m(x)\,\Delta x - m(y) \,\Delta x.$

$\displaystyle f(x)$-nek ott van szélsőértéke, ahol az $\displaystyle x$ kis változtatására az értéke nem változik. Ez nyilván teljesül abban a pontban, ahol

$\displaystyle y=\frac{(1-x)}{2}=x ,\qquad \mbox{azaz} \qquad x=\frac{1}{3}.$

Mivel az $\displaystyle f(x)$-ben a négyzetgyök alatt álló kifejezés egy lefelé nyíló parabolának felel meg, $\displaystyle f(x)$ konkáv függvény, tehát $\displaystyle f$-nek csak $\displaystyle x=\tfrac13$-nál van szélsőértéke, és az egy maximum. Ez tehát a keresett magasság érték, és ha a hordókon a lyukak így helyezkednek el, a borsugarak becsapódási pontja között a távolság

$\displaystyle \ell_\text{max}=d+ 2\sqrt{2}h.$

5. módszer. $\displaystyle f(x)$ két tag összege. Jelöljük ezeket

$\displaystyle u(x)=\sqrt{x(1-x)}\qquad \text{és}\qquad v(x)= \sqrt{1-x^2}$

módon, és ábrázoljuk a függvények grafikonját az $\displaystyle (x,u)$ és $\displaystyle (x,v)$ derékszögű koordináta-rendszerekben. Négyzetre emelés és teljes négyzetté alakítás után kapjuk, hogy

$\displaystyle \left(x-\frac12\right)^2+u^2=\left(\frac12\right)^2,$

illetve

$\displaystyle x^2+v^2=1.$

Látjuk, hogy mindkét görbe kör, pontosabban a 2. ábrán folytonos vonallal jelölt körív, hiszen

$\displaystyle 0\le x\le 1,\quad u\ge 0 \qquad\text{és}\qquad v\ge0.$

2. ábra

$\displaystyle f(x)=u(x)+v(x)$ maximumát keressük. Legyen $\displaystyle u(x)$ meredeksége (az érintőjének iránytangense az $\displaystyle x$ absszciszájú helyen $\displaystyle m_1(x)$, $\displaystyle v(x)$ meredeksége pedig $\displaystyle m_2(x)<0$. Keressük meg azt az $\displaystyle x_0$ értéket, amelynél

$\displaystyle m_1(x_0)=-m_2(x_0)=m_0,$

vagyis $\displaystyle f(x)$ növekedési üteme éppen nulla. A 2. ábráról leolvashatjuk, hogy egyrészt

$\displaystyle \sin\varphi=\frac{\tfrac12-x_0}{\tfrac12},$

másrészt

$\displaystyle \sin\varphi=x_0,$

vagyis

$\displaystyle 1-2x_0=x_0, \qquad \text{azaz}\qquad x_0=\frac13.$

(Kihasználtuk, hogy a kisebb kör sugara $\displaystyle 1/2$, a nagyobbé 1, és az érintők merőlegesek a körök megfelelő sugarára.)

A 2. ábráról azt is leolvashatjuk, hogy $\displaystyle x<x_0$ esetén

$\displaystyle m_1(x)>m_0 \qquad \text{és} \qquad m_2(x)>-m_0,\qquad \text{tehát} \qquad m_1(x)+m_2(x)>0,$

$\displaystyle x>x_0$ esetén pedig

$\displaystyle m_1(x)<m_0 \qquad \text{és} \qquad m_2(x)<-m_0,\qquad \text{vagyis} \qquad m_1(x)+m_2(x)<0.$

Ezek szerint $\displaystyle f(x)$ monoton növekszik, amikor $\displaystyle x<x_0$, és monoton csökken, ha $\displaystyle x>x_0,$ tehát $\displaystyle x_0$-nál maximuma van.

6. módszer. Induljunk ki most is az $\displaystyle f(x)$ függvény két tagjának megfelelő körökből. Olyan $\displaystyle x_0$ abszcisszájú pontokat keresünk, amelyhez tartozó érintők meredekségének nagysága megegyezik, csak az előjelük különböző. A 3. ábra vázlatosan mutatja, hogy három egyszerű geometriai transzformációval a (színesen jelölt) kis kört átvihetjük (áttranszformálhatjuk) a nagyobb körbe.

3. ábra

A tükrözés az $\displaystyle m$ meredekséget $\displaystyle (-m)$-re változtatja, az eltolás és a nagyítás pedig nem változtatja meg az érintő meredekségét. Ha olyan $\displaystyle x_0$ értéket választunk, amely a három transzformáció után éppen a kiindulási $\displaystyle x_0$ értékkel egyezik meg, akkor megtaláltuk $\displaystyle f(x)$ nulla meredekségű pontját, ami a keresett maximum helye.

$\displaystyle 1-2x_0=x_0, \qquad \text{vagyis}\qquad x_0=\frac13.$

A hordókat tehát a magasságuk alsó egyharmadánál kell megfúrni, akkor lesz legnagyobb a borsugarak becsapódási pontjai közötti távolság.

Statisztika:

75 dolgozat érkezett.
5 pontot kapott:	54 versenyző.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	4 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2023. novemberi fizika feladatai