 |
A P. 5521. feladat (2023. november) |
P. 5521. Egy főzőlapon 12 egyforma ellenálláshuzal található, amelyek az ábrán látható módon kapcsolódnak egymáshoz.
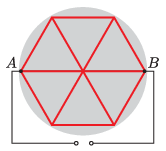
Milyen a főzőlap hőteljesítményének százalékos megoszlása az egyes huzalok között, ha az \(\displaystyle A\) és \(\displaystyle B\) pontok közé feszültséget kapcsolunk?
Közli: Tornyos Tivadar Eörs, Budapest
(4 pont)
A beküldési határidő 2023. december 15-én LEJÁRT.
Megoldás. A teljesítmények százalékos megoszlása nem függ sem a hálózatra kapcsolt \(\displaystyle U\) feszültségtől, sem az ellenálláshuzalok \(\displaystyle R\) ellenállásától, hiszen mindegyik részteljesítmény \(\displaystyle U^2/R\)-rel arányos. Legyen pl. \(\displaystyle U=8\ \rm V\) és \(\displaystyle R=1\ \Omega\). (A továbbiakban az SI mértékegységeket nem írjuk ki.)
Ha az \(\displaystyle A\) pont potenciálja \(\displaystyle -4\), a \(\displaystyle B\) ponté \(\displaystyle +4\), akkor a középpont potenciálja (a szimmetria miatt) nulla. A másik két pont potenciálja (ugyancsak a szimmetria miatt) \(\displaystyle \pm x\) (1. ábra). (\(\displaystyle x\) értékét most még nem ismerjük.)
1. ábra
2. ábra
Az áramerősségek (\(\displaystyle R=1\) miatt) az egyes ellenálláshuzalok végpontjainak potenciálkülönbségével egyenlő (2. ábra). A felső és az alsó ágak bármelyik csomópontjára felírható Kirchhoff-törvény szerint
\(\displaystyle 4-x=x+2x,\qquad \text{vagyis}\qquad x=1.\)
Az áramerősségek négyzetével megegyező teljesítményeket, illetve azok százalékos megoszlását a (3. ábra) mutatja.
3. ábra
Statisztika:
37 dolgozat érkezett. 4 pontot kapott: Barna Márton, Bogdán Benedek, Bunford Luca, Csapó András, Csóka Péter, Fehérvári Donát, Fekete Lúcia, Gerendás Roland, Hüvös Gergely, Képes Botond, Kis Márton Tamás, Klement Tamás, Molnár Kristóf, Muraközi Péter, Sipeki Árpád, Szabó Donát, Tibor Varga, Žigo Boglárka. 3 pontot kapott: Benes András, Fórizs Borbála, Tóth Kolos Barnabás. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 10 versenyző.
A KöMaL 2023. novemberi fizika feladatai