 |
A P. 5522. feladat (2023. november) |
P. 5522. Két vízszintes, párhuzamos, súrlódásmentes szigetelőrúd egymástól \(\displaystyle d\) távolságra helyezkedik el. Az alsó rúdon egy \(\displaystyle q\) töltésű, \(\displaystyle m\) tömegű, a felsőn pedig egy \(\displaystyle -q\) töltésű, \(\displaystyle m\) tömegű kicsiny szigetelőgyöngy csúszik az ábrán látható módon.
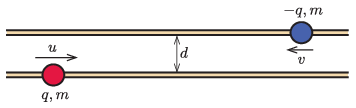
Kezdetben a gyöngyök egymástól távol helyezkednek el, és \(\displaystyle u\) illetve \(\displaystyle v\) nagyságú sebességgel indulnak egymás felé. Mekkora lesz a mozgás során az egyes testek maximális sebessége?
Közli: Németh Róbert, Budapest
(5 pont)
A beküldési határidő 2023. december 15-én LEJÁRT.
Megoldás. A mozgás egy adott \(\displaystyle t\) időpillanatában a gyöngyök egymás fölé érnek, ekkor a köztük ható erőnek nem lesz vízszintes komponense, így itt lesz sebességük maximális, jelölje ezeket a sebességeket \(\displaystyle U\) illetve \(\displaystyle V\).
Az általánosság elvesztése nélkül feltehetjük, hogy \(\displaystyle u>v\). Mivel csak belső erők hatnak, a rendszer teljes impulzusa időben állandó; specifikusan igaz ez a kezdeti állapot és a \(\displaystyle t\) időpont között is:
| \(\displaystyle (1) \) | \(\displaystyle mu - mv = mU - mV\,.\) |
Hasonlóan az energiamegmaradás törvénye is felírható a Coulomb-erő konzervatív voltából fakadóan:
| \(\displaystyle (2) \) | \(\displaystyle \frac{1}{2}mu^2 + \frac{1}{2}mv^2 = \frac{1}{2}mU^2 + \frac{1}{2}mV^2 - \frac{kq^2}{d}\,.\) |
Az (1) egyenletből \(\displaystyle V = U - u + v\), amelyet a (2) kifejezésbe behelyettesítve:
\(\displaystyle U^2 -(u-v)U - uv - \frac{kq^2}{md} = 0\,. \)
A másodfokú egyenlet megoldóképlete alapján végül adódik az \(\displaystyle U\) sebesség. A két matematikai megoldás közül az \(\displaystyle u>v\) feltevésünket figyelembe véve a pozitívat kell választani:
\(\displaystyle {U = \frac{u-v}{2} + \sqrt{\frac{(u+v)^2}{4} + \frac{kq^2}{md}} }\,. \)
A másik matematikai megoldás pedig éppen a \(\displaystyle V\) sebesség ellentettjének felel meg a kiindulóegyenletek szimmetriájából fakadóan:
\(\displaystyle {V = \frac{v-u}{2} + \sqrt{\frac{(u+v)^2}{4} + \frac{kq^2}{md}} }\,. \)
Statisztika:
44 dolgozat érkezett. 5 pontot kapott: Csapó András, Csiszár András, Csóka Péter, Czirják Márton Pál, Flóring Balázs, Hegedüs Márk, Képes Botond, Klement Tamás, Muraközi Péter, Szabó Donát. 4 pontot kapott: Bélteki Teó, Bencz Benedek, Bernhardt Dávid, Debreceni Dániel, Dobos Anita, Fajszi Karsa, Masa Barnabás, Molnár Zétény, Seprődi Barnabás Bendegúz, Tárnok Ede , Tóth Kolos Barnabás, Zólomy Csanád Zsolt. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 9 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2023. novemberi fizika feladatai

