A P. 5528. feladat (2023. december)

P. 5528. Vízszintes, súrlódásmentesnek tekinthető talajon egy $\displaystyle d=10~\mathrm{cm}$ oldalélű, homogén tömegeloszlású kocka csúszik $\displaystyle v_0$ sebességgel. Egyszer csak a kocka a talajhoz csatlakozó, $\displaystyle \alpha=30^\circ$ hajlásszögű lejtőhöz ér. A lejtő és a talaj ,,törésvonala'' merőleges a kocka haladási irányára. A kocka talajjal érintkező, első oldaléle a törésvonalnál tökéletesen rugalmatlanul megakad, így a kocka megbillen. Legalább mekkora $\displaystyle v_0$ értéke, ha a kocka elülső oldallapja ,,rábillen'' a lejtőre?

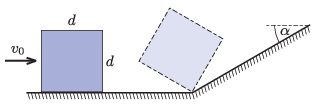
Közli: Vigh Máté, Biatorbágy

(5 pont)

A beküldési határidő 2024. január 15-én LEJÁRT.

Megoldás. A megbillenő kocka az ütközés után a törésvonal, mint forgástengely körül valamekkora $\displaystyle \omega$ szögsebességgel kezd el forogni. A lejtőre történő ,,ráborulás'' feltétele az, hogy $\displaystyle 45^\circ$-os szögelfordulása után a mozgási energiája pozitív (határesetben nulla) legyen.

A homogén tömegeloszlású kocka bármelyik élére vonatkoztatott tehetetlenségi nyomatéka $\displaystyle \Theta=\frac23md^2$. (Ezt pl. a táblázatokban megtalálható tömegközéppontra vonatkoztatott tehetetlenségi nyomatékból a Steiner-tétel alkalmazásával kaphatjuk meg.)

Az ütközés utáni kezdeti szögsebességet a perdületmegmaradás tételének alkalmazásával határozhatjuk meg. A kocka kezdeti (a tömegközéppont mozgásából adódó) perdülete a törésvonalra vonatkoztatva $\displaystyle mv_0d/2$, ütközés után pedig $\displaystyle \Theta\omega$. Mivel az ütközés során fellépő erők hatásvonala a törésvonalon halad keresztül, ezek eredő forgatónyomatéka nulla, és így a perdület változatlan marad:

$\displaystyle mv_0\frac{d}2=\frac23md^2\omega,$

ahonnan

$\displaystyle \omega=\frac34\frac{v_0}{d}.$

A kocka mozgási energiája közvetlenül az ütközés után

$\displaystyle E=\frac{1}{2}\Theta\omega^2=\frac{3}{16}mv_0^2.$

Ennek az energiának kell fedeznie a gravitációs helyzeti energia növekedését az ,,éppen átbillenés'' határesetében:

$\displaystyle \frac{3}{16}mv_0^2\ge mg\left(\frac{\sqrt2 d }{2}-\frac{d}{2}\right).$

Innen az átbillenéshez szükséges sebesség:

$\displaystyle v_0>\sqrt{\frac83\left(\sqrt2-1\right)gd}\approx 1{,}04\ \frac{\rm m}{\rm s}.$

Statisztika:

51 dolgozat érkezett.
5 pontot kapott:	Bogdán Benedek, Csapó András, Csiszár András, Czirják Márton Pál, Fekete Lúcia, Hegedüs Márk, Kis Márton Tamás, Kiss 131 Adorján Timon, Medgyesi Júlia, Molnár Kristóf, Molnár Zétény, Sipeki Árpád, Tárnok Ede .
4 pontot kapott:	Seprődi Barnabás Bendegúz.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	10 versenyző.
1 pontot kapott:	16 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2023. decemberi fizika feladatai