A P. 5530. feladat (2023. december)

P. 5530. Egy orvosi fecskendő dugattyújának $\displaystyle 300~\mathrm{mm^2}$, kivezető csöve üregének pedig $\displaystyle 4~\mathrm{mm^2}$ a keresztmetszete. A nyitott végű eszköz dugattyújának megmozdításához (a tapadási súrlódás legyőzéséhez) $\displaystyle 1{,}4~\mathrm{N}$ erő szükséges. Miután a kivezető csövet az ábra szerint egyik ujjunkkal befogtuk, a dugattyút egy másik ujjunkkal nagyon lassan befelé toljuk úgy, hogy egyéb helyen nem érünk a végig nyugalomban lévő fecskendőhöz (lásd az ábrát). A teljes folyamat során a bezárt levegő térfogata $\displaystyle 20~\mathrm{cm^3}$-ről $\displaystyle 15~\mathrm{cm^3}$-re csökken.

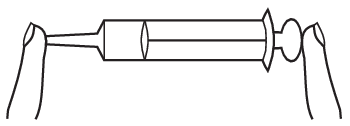
$\displaystyle a$) Mennyi a dugattyú betolását követően a bezárt levegő nyomása?

$\displaystyle b$) Legalább mekkora erővel kell szorítanunk ekkor a fecskendő kivezető csövének végét?

(A külső légnyomás $\displaystyle 100~\mathrm{kPa}$, a fecskendő súlyától eltekinthetünk.)

Közli: Kis Tamás, Heves

(4 pont)

A beküldési határidő 2024. január 15-én LEJÁRT.

Megoldás. $\displaystyle a)$ Ha a levegőt nagyon lassan nyomjuk össze, a hőmérséklete állandó marad, nyomása pedig a folyamat végén a Boyle–Mariotte-törvény szerint:

$\displaystyle p = 100\,\textrm{kPa}\ \frac{20\,\textrm{cm}^3}{15\,\textrm{cm}^3} = 133\,\textrm{kPa}$

$\displaystyle b)$ A fecskendő két végét nyilván ugyanakkora erővel nyomjuk (nem gyorsul). A dugattyú felőli erőt egyszerűbb meghatározni ezért foglalkozzunk azzal! Jelöljük a külső légnyomást $\displaystyle p_0$-lal, és a dugattyú keresztmetszetét $\displaystyle A$-val. SI mértékegységekben $\displaystyle p_0=10^5\,\mathrm{Pa}$, $\displaystyle A=3\cdot 10^{-4}\,\mathrm{m}^2$; a fecskendőben levő levegő nyomása $\displaystyle \tfrac{4}{3}p_0$.

A dugattyút a levegő minden oldalról nyomja de az eredő nyomóerőt úgy is helyesen megkapjuk, ha csak a $\displaystyle p_0$-hoz képesti túlnyomást vesszük figyelembe:

$\displaystyle \Delta p=\frac{4}{3}\,p_0-p_0=\frac{1}{3}\,p_0\,.$

A dugattyúra ható, levegő nyomásából származó erő tehát

$\displaystyle A\,\Delta p =3\cdot 10^{-4}\,\mathrm{m}^2\cdot\frac{1}{3}\cdot 10^5\,\mathrm{Pa}=10\,\mathrm{N}\,.$

A dugattyú helyben tartásában segít még az $\displaystyle 1{,}4\,\mathrm{N}$ nagyságú tapadási súrlódási erő, ezért végül csak

$\displaystyle 10\,\mathrm{N}-1{,}4\,\mathrm{N}=8{,}6\,\mathrm{N}$

erővel kell a fecskendőt tartanunk.

Megjegyzés. A kivezető csőnél az erő egy részét a cső, másik részét a belül lévő túlnyomásos levegő fejti ki. A kettő együtt éppen kioltja a másik oldalon kifejtett erőt. A kivezető cső belső keresztmetszetére nem volt szükség.

Statisztika:

63 dolgozat érkezett.
4 pontot kapott:	Barna Márton, Bunford Luca, Éger Viktória, Fekete Lúcia, Flóring Balázs, Fórizs Borbála, Gerendás Roland, Képes Botond, Molnár Ábel, Molnár Kristóf, Papp András, Sütő Áron, Szabó Donát, Vágó Botond, Zólomy Csanád Zsolt.
3 pontot kapott:	Bélteki Teó, Boér Panna Rita, Erős Fanni, Hornok Máté, Magyar Zsófia, Süveg Janka Villő, Szécsényi-Nagy Rudolf, Tóth Hanga Katalin.
2 pontot kapott:	28 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2023. decemberi fizika feladatai