A P. 5534. feladat (2023. december)

P. 5534. Legyen egy derékszögű koordináta-rendszer $\displaystyle x$ tengelye vízszintes, $\displaystyle y$ tengelye pedig függőleges. Az $\displaystyle x$ tengely $\displaystyle 0\le \xi\le h=1~\mathrm{m}$ minden egyes $\displaystyle x=\xi$ pontját kössük össze az $\displaystyle y$ tengelyen lévő $\displaystyle y=h-\xi$ ponttal. Fektessünk egy súrlódásmentes, vékony csövet az előzőek szerint felvett szakaszokból kialakuló sárga ,,síkidom'' burkolójára.

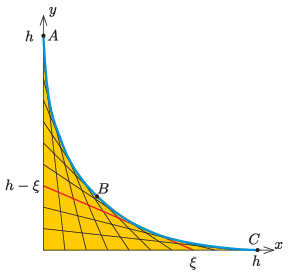
Indítsunk el lökésmentesen egy $\displaystyle m$ tömegű, kicsiny testet a cső tetejéről. Adjuk meg $\displaystyle mg$ egységekben, hogy a mozgása során mekkora erővel nyomja a test a cső falát

$\displaystyle a)$ közvetlenül az indulás után az $\displaystyle A$ pontban;

$\displaystyle b)$ a cső $\displaystyle B$ felezőpontjánál;

$\displaystyle c)$ közvetlenül a cső elhagyása előtt a $\displaystyle C$ pontnál!

Közli: Honyek Gyula, Veresegyház

(6 pont)

A beküldési határidő 2024. január 15-én LEJÁRT.

Megoldás. A megoldáshoz a következő lépések vezetnek el:

– Meghatározzuk a burkológörbe alakját;

– kiszámítjuk a kis test sebességét a kérdéses pontokban;

– meghatározzuk a cső görbületi sugarát a szóban forgó pontokban;

– és végül felírjuk a test Newton-féle mozgásegyenletét a burkológörbe érintőjére merőleges irányba, amiből megkapjuk a kérdezett nyomóerőt.

1. A burkológörbe meghatározása.

A $\displaystyle \xi$ paraméterhez tartozó egyenes egyenlete:

Tekintsünk egy adott $\displaystyle (x,y)$ koordinátákkal rendelkező $\displaystyle P$ pontot, és számítsuk ki, hogy mekkora $\displaystyle \xi$ érték(ek)hez tartozó egyenes(ek) halad(nak) át ezen a ponton. Az ábrán is látszik, hogy ha $\displaystyle P$ a sárga tartományba esik, akkor két egyenes halad át rajta, ha $\displaystyle P$ a kék burkológörbén helyezkedik el, akkor csak egy (a burkolót érintő) egyenes halad át rajta, a fehér tartományba eső pontoknál pedig egyetlen $\displaystyle \xi$ sem elégíti ki az (1) egyenletet. Fejezzük ki $\displaystyle \xi$-t (1)-ből:

Ennek a másodfokú egyenletnek akkor van pontosan 1 megoldása, ha az egyenlet diszkriminánsa nulla:

$\displaystyle (y-x-h)^2-4xh=0,$

amit így is felírhatunk:

Belátjuk, hogy (3) egy olyan parabola egyenlete, amelynek szimmetriatengelye az $\displaystyle x$ tengellyel $\displaystyle 45^\circ$-os szöget zár be.

Az $\displaystyle (x,y)$ és a hozzá képest $\displaystyle 45^\circ$-kal elforgatott $\displaystyle (X,Y)$ koordináta-rendszerek kapcsolata az 1. ábráról olvasható le:

$\displaystyle X=\frac{x-y}{\sqrt2}, \qquad Y=\frac{x+y}{\sqrt2}.$

1. ábra

Ennek megfelelően a burkológörbe egyenlete:

ami valóban egy parabolát ír le.

2. A test sebességének meghatározása.

A test kezdősebessége $\displaystyle v_A=0.$ A $\displaystyle \xi=h/2$ paraméterhez tartozó $\displaystyle B$ pont koordinátái: $\displaystyle x_B=y_B=h/4$, a $\displaystyle \xi=h$ értéknek megfelelő $\displaystyle C$ ponté pedig $\displaystyle x_C=h$ és $\displaystyle y_C=0$.

Írjuk fel az energiamegmaradás törvényét az $\displaystyle A$ és $\displaystyle B$, valamint az $\displaystyle A$ és $\displaystyle C$ pontok közötti mozgásra:

valamint

3. Görbületi sugarak kiszámítása.

Egy síkgörbe simulókörének sugara (vagy ennek reciproka: a görbület) többféleképpen is meghatározható. Felsőbb matematikai módszerekkel (differenciálszámítással) a görbe egyenletéből közvetlenül megkaphatjuk a keresett sugár nagyságát, de elemi úton, fizikai (optikai vagy pontmechanikai) megfontolásokkal is célhoz érhetünk.

Tekintsük a feladatban szereplő elrendezést egy forgásparaboloid alakú tükör síkbeli metszetének (2. ábra).

2. ábra

A tükör $\displaystyle C$ pontjához érkező, a parabola tengelyével párhuzamos, tehát $\displaystyle 45^\circ$-os beesési szögű fénysugár $\displaystyle 45^\circ$-os szögben verődik vissza, az $\displaystyle A$ pont irányába halad. Az optikai tengelyt a $\displaystyle (h/2, h/2)$ koordinátájú $\displaystyle F$ pontban éri el, ez a pont tehát a tükör fókuszpontja. A $\displaystyle BF=f_B$ távolság $\displaystyle h/2\sqrt{2}$, és – a gömbtükör ismert tulajdonságai miatt – ennek kétszerese a parabola görbületi sugara a $\displaystyle B$ pontban:

Megjegyzés. A parabola vezéregyenese az optikai tengelyre merőleges, tehát $\displaystyle AC$-vel párhuzamos, az origón áthaladó egyenes.

Hasonló megfontolásokkal kapjuk meg a $\displaystyle C$ ponthoz tartozó görbületi sugár nagyságát is. A $\displaystyle C$ közelébe érkező párhuzamos sugárnyaláb is az $\displaystyle F$ pontban fókuszálódik, ilyen sugarakra tehát a fókusztávolság $\displaystyle f_C=h/\sqrt2$. Egy $\displaystyle R_C$ sugarú gömbtükörre nem merőlegesen, hanem $\displaystyle \alpha$ beesési szögben érkező fénysugarakra a leképezési törvény:

$\displaystyle \frac{1}{t}+\frac{1}{k}=\frac{2}{R_C\,\cos\alpha}$

(lásd Kós Géza: Lehet egy közelítéssel kevesebb? c. cikkét a Kömal 2010. évi 3. számának 174-180. oldalán, http://db.komal.hu/KomalHU/). Esetünkben $\displaystyle 1/t=0$, $\displaystyle \alpha=45^\circ$ és $\displaystyle k=f_C=h/\sqrt2$, ahonnan

(Nyilván ugyanekkora $\displaystyle R_A$ is, de erre nincs szükségünk.)

A görbületi sugarakat nemcsak optikai megfontolásokkal, hanem a vízszintes hajítás képleteiből is megkaphatjuk. Fordítsuk el (és tükrözzük) az $\displaystyle (X,Y)$ koordináta-rendszert úgy, hogy az $\displaystyle Y$ tengely mutasson függőlegesen lefelé (3. ábra).

3. ábra

Tegyük fel a következő kérdést: Mekkora $\displaystyle v_0$ nagyságú, vízszintes irányú kezdősebességgel kell elhajítanunk egy kicsiny testet, hogy annak pályagörbéje éppen a (4) egyenlettel megadott legyen? Mivel

$\displaystyle X=v_0t \qquad \text{és}\qquad Y=\frac{h}{2\sqrt2}+\frac{g}2t^2,$

a pálya egyenlete

$\displaystyle Y= \frac{h}{2\sqrt2}+\frac{g}{2v_0^2} X^2.$

Ezt (4)-gyel összevetve leolvashatjuk, hogy

$\displaystyle v_0^2=\frac{gh}{\sqrt2}.$

Tudjuk, hogy a test gyorsulása mindenhol $\displaystyle g$, így a $\displaystyle B$ pontban is, ami akkor egyezik meg a $\displaystyle v_0^2/R_B$-vel, ha $\displaystyle R_B=h/\sqrt2$, ahogy azt már (7)-ben megkaptuk.

A $\displaystyle C$ pontban, ahol a pályagörbe meredeksége $\displaystyle -1$, a hajítás törvényei szerint $\displaystyle v_C^2=\sqrt{2}gh$, a centripetális gyorsulása tehát

$\displaystyle \frac{v_C^2}{R_C}=\frac{\sqrt2 gh}{R_C}=g\cos45^\circ=\frac{g}{\sqrt2}.$

Innen kapjuk, hogy $\displaystyle R_C=2h,$ összhangban (8)-cal.

4. A nyomóerők meghatározása.

Most, hogy ismerjük a test sebességét és a pálya görbületi sugarát a kritikus pontokban, könnyen kiszámíthatjuk a cső által kifejtett nyomóerőket is. Ha a pálya valamelyik pontjában a görbe normálisa (az érintőjére merőleges irány) $\displaystyle \alpha$ szöget zár be a vízszintessel, a test sebessége $\displaystyle v$ és a görbületi sugár $\displaystyle R$, akkor (lásd a 4. ábrát) a Newton-egyenlet szerint

$\displaystyle N-mg\cos\alpha=\frac{mv^2}{R},$

vagyis

$\displaystyle N=mg\cos\alpha+\frac{mv^2}{R}.$

4. ábra

$\displaystyle a)$ Az $\displaystyle A$ pontnál $\displaystyle \alpha=90^\circ$ és $\displaystyle v_A=0$, így $\displaystyle N_A=0.$

$\displaystyle b)$ A $\displaystyle B$ pontnál $\displaystyle \alpha=45^\circ$, $\displaystyle v_B=\sqrt{\tfrac32gh}$ és $\displaystyle R_B=\tfrac{h}{\sqrt2}$, ennek megfelelően $\displaystyle N_B=2\sqrt2\,mg\approx 2{,}8\,mg$.

$\displaystyle c)$ Végül a pálya legalsó, $\displaystyle C$ pontjánál $\displaystyle \alpha=0^\circ$, $\displaystyle v_C=\sqrt{2gh}$ és $\displaystyle R_C=2h$, így $\displaystyle N_C=2mg$.

(Látható, hogy a nyomóerők és $\displaystyle mg$ aránya nem függ $\displaystyle h$ konkrét értékétől.) A fentebb kiszámított $\displaystyle N$ erőket a cső fejti ki a lecsúszó testre. A kis test által a csőre kifejtett erők $\displaystyle N$ ellenerejei.

Statisztika:

24 dolgozat érkezett.
6 pontot kapott:	Bencz Benedek, Csapó András, Csóka Péter, Czirják Márton Pál, Fajszi Karsa, Fehérvári Donát, Gyenes Károly, Képes Botond, Kiss 131 Adorján Timon, Tóth Kolos Barnabás.
3 pontot kapott:	2 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2023. decemberi fizika feladatai