A P. 5537. feladat (2024. január)

P. 5537. Egy kalandparkban az erre vállalkozók egy $\displaystyle R\!=\!20~\text{m}$ magas, $\displaystyle {\alpha\!=\!30^{\circ}}$-os hajlásszögű lejtő tetejéről ($\displaystyle A$), kezdősebesség nélkül, szabadon (fékezésmentesen) gurulhatnak lefelé egy kicsiny kocsiban. A lejtő törésmentesen csatlakozik egy $\displaystyle R$ sugarú, körív alakú pályaszakaszhoz ($\displaystyle B$), majd a pálya a legmélyebb pontjától ($\displaystyle C$) vízszintesen folytatódik tovább. A vízszintes szakaszon a megfelelő módon fékezett kocsi időben egyenletesen lassul, és $\displaystyle \ell=2R$ út megtétele után a $\displaystyle D$ pontnál megáll.

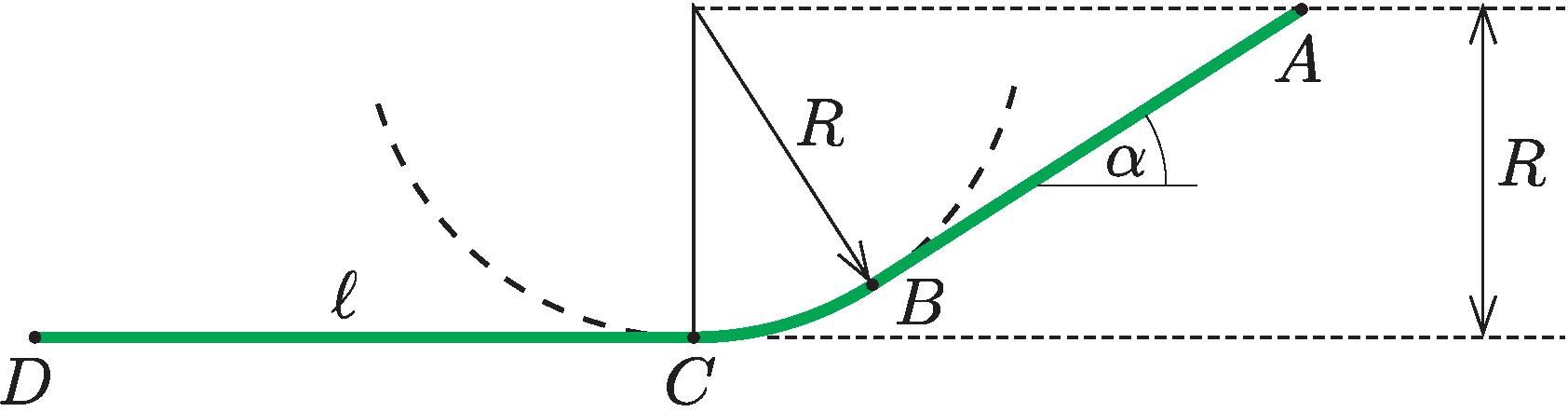
Számítsuk ki, hogy az utasok a szokásos súlyuknak hányszorosát érzik a mozgásuk során! Ábrázoljuk ezt az arányt a megtett út függvényében!

Holics László feladata nyomán

(5 pont)

A beküldési határidő 2024. február 15-én LEJÁRT.

Megoldás. Ha egy $\displaystyle m$ tömegű testre a nehézségi erőn kívül $\displaystyle \boldsymbol{K}$ erő hat, akkor a mozgásegyenlet szerint

$\displaystyle m\boldsymbol{g}+\boldsymbol{K}=m\boldsymbol{a},$

vagyis

$\displaystyle \boldsymbol{K}=m(\boldsymbol{a}-\boldsymbol{g}),$

ahol $\displaystyle \boldsymbol{a}$ a test gyorsulásvektora. Megállapodás szerint a $\displaystyle \boldsymbol{K}$ erő ellenerejének nagyságát nevezik a test $\displaystyle G$ súlyának:

$\displaystyle G=m\vert\boldsymbol{g}-\boldsymbol{a}\vert.$

(Ezt a $\displaystyle G$ értéket mutatja az a mérleg, amit a gyorsuló test alá helyeznek.) A szokásos súly az álló helyzetben (vagy gyorsulásmentes körülmények között) mért súly: $\displaystyle G_0=mg.$ A feladatban kérdezett arányszám:

$\displaystyle \lambda\equiv\frac{G}{G_0}=\frac{\vert\boldsymbol{g}-\boldsymbol{a}\vert}{g}.$

I. Az $\displaystyle A$ és $\displaystyle B$ pont között a kis kocsi (és benne az emberek) lejtőirányú gyorsulása $\displaystyle a=g\sin\alpha$. Ugyanekkora a nehézségi erő lejtőirányú komponense is, ezek különbsége tehát nulla. Ennek megfelelően

$\displaystyle \vert\boldsymbol{g}-\boldsymbol{a}\vert=g\cos\alpha$

és így

$\displaystyle \lambda=\cos\alpha\approx 0{,}87.$

A mozgás ezen szakaszának hossza

$\displaystyle s_1=R\,\ctg\alpha\approx 34{,}6\,\mathrm{m}.$

II. A mozgás második szakaszában (a $\displaystyle CB$ köríven) a test gyorsulása az érintőirányú gyorsulásból és a sugárirányú (centripetális) gyorsulásból tevődik össze. Az érintőleges gyorsulás és a nehézségi gyorsulás érintőirányú komponense megegyezik, ezek különbsége tehát nulla. A sugárirányú gyorsulás nagysága $\displaystyle v^2/R$, ahol $\displaystyle v$ a test pillanatnyi sebessége. A nehézségi gyorsulás sugárirányú komponense a centripetális gyorsulással ellentétes irányú és $\displaystyle g\cos\varphi$ nagyságú, ahol $\displaystyle \varphi$ ($\displaystyle \alpha>\varphi>0)$ a test pillanatnyi helyzetéhez tartozó sugárnak a függőlegessel bezárt szöge. Ennek megfelelően

$\displaystyle \lambda=\frac{v^2}{Rg}+\cos\varphi.$

A sebességet az energiamegmaradás törvényét alkalmazva kapjuk meg:

$\displaystyle \frac{1}{2}mv^2=mgR\cos\varphi,\qquad\textrm{vagyis}\qquad v=\sqrt{2gR\cos\varphi},$

és innen

$\displaystyle \lambda=3\cos\varphi.$

A körív hossza:

$\displaystyle s_2=R\alpha=R\frac{\pi}{6}\approx 10{,}5\,\mathrm{m}.$

Közvetlenül a $\displaystyle B$ pont elhagyása után $\displaystyle \lambda\approx 2{,}6$, a $\displaystyle C$ pont elérése előtti pillanatban pedig $\displaystyle \lambda=3{,}00.$ A megtett $\displaystyle s$ út és $\displaystyle \varphi$ közötti kapcsolat:

$\displaystyle \varphi=\ctg\alpha+\alpha-\frac{s}{R}.$

III. A mozgás harmadik, fékezéses szakaszában a gyorsulás vízszintes irányú és $\displaystyle a=\frac{R}{\ell}g=\frac{1}{2}g$ nagyságú. Ennek megfelelően

$\displaystyle \lambda=\frac{\sqrt{5}}{2}\approx 1{,}12.$

A mozgás ezen szakaszának hossza $\displaystyle s_3=40\,\mathrm{m}$, a teljes út pedig $\displaystyle s_1+s_2+s_3\approx 85\,\mathrm{m}.$

A $\displaystyle \lambda$ arányszámnak a megtett úttól való függését az ábra mutatja. Látható, hogy $\displaystyle \lambda(s)$ nem folytonos függvény, a $\displaystyle B$ és a $\displaystyle C$ pontokban ,,ugrása'' van. A Newton-törvény szerint (véges nagyságú erők esetén) csak a sebesség nem változhat meg hirtelen, a gyorsulásra nincs ilyen kikötés.

Megjegyzés. A feladatban leírt ,,zökkenés'' elkerülése érdekében a vasúti pályák és az autópályák görbületi sugara csak fokozatosan változik, tehát egyesen szakaszhoz sosem csatlakozik körív.

Statisztika:

40 dolgozat érkezett.
5 pontot kapott:	Bernhardt Dávid, Csiszár András, Fehérvári Donát, Hegedüs Márk, Nguyen Kim Dorka, Tóth Kolos Barnabás, Vágó Botond, Zólomy Csanád Zsolt.
4 pontot kapott:	Bélteki Teó, Bencze Mátyás, Csapó András, Czirják Márton Pál, Debreceni Dániel, Fajszi Karsa, Gyerő Soma, Kovács Kristóf , Seprődi Barnabás Bendegúz, Sütő Áron, Szabó Donát, Tárnok Ede , Zádori Gellért, Žigo Boglárka.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2024. januári fizika feladatai