A P. 5542. feladat (2024. január)

P. 5542. Egy \(\displaystyle R\) ellenállásból, egy \(\displaystyle L\) induktivitású tekercsből, egy \(\displaystyle C\) kapacitású kondenzátorból és egy \(\displaystyle U(t)=U_0\sin(\omega t)\) feszültségű generátorból az ábrán látható egyszerű áramkört hozzuk létre.

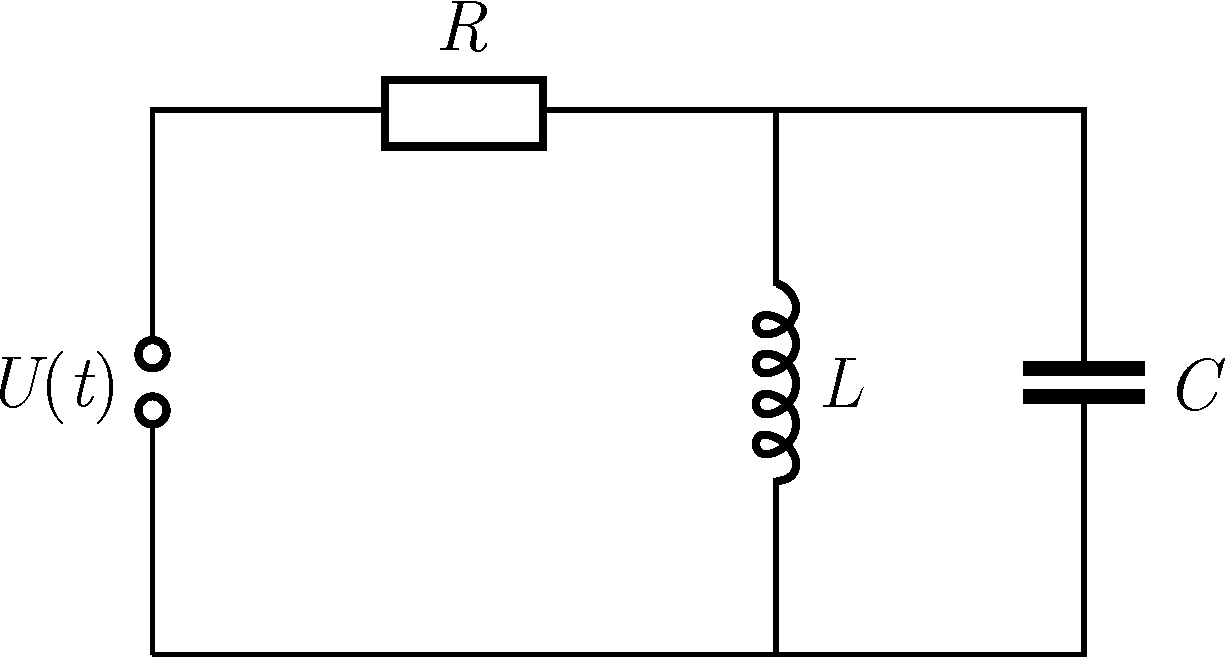
\(\displaystyle a)\) Mekkora az ellenálláson átfolyó áram amplitúdója?

\(\displaystyle b)\) Hogyan válasszuk meg az \(\displaystyle \omega\) körfrekvenciát ahhoz, hogy az ellenálláson ne folyjon áram?

Közli: Németh Róbert, Budapest

(5 pont)

A beküldési határidő 2024. február 15-én LEJÁRT.

I. megoldás. \(\displaystyle a)\) Ha a párhuzamos \(\displaystyle LC\)-körre jutó feszültség csúcsértéke \(\displaystyle U_1\), akkor a tekercsen

\(\displaystyle I_1=\frac{U_1}{L\omega}\)

erősségű, a kapocsfeszültséghez képest \(\displaystyle 90^\circ\)-kal késő áram folyik. Ugyanakkor a kondenzátoron

\(\displaystyle I_2=U_1\,\omega C\)

erősségű, a kapocsfeszültséghez képest \(\displaystyle 90^\circ\)-kal siető áram folyik. A két áram előjeles összegének nagysága (mivel azok egymáshoz képest \(\displaystyle 90^\circ+90^\circ=180^\circ\) fázistolásban vannak):

\(\displaystyle I=\vert I_1-I_2\vert =U_1\left|\frac{1}{L\omega}-\omega C\right|.\)

Ez a két (párhuzamosan kapcsolt) áramköri elem tehát az adott körfrekvencián \(\displaystyle L\omega>\frac{1}{\omega C} \) esetén helyettesíthető egyetlen tekerccsel, ellenkező esetben pedig egyetlen kondenzátorral. Bármelyik eset teljesül, az egész áramkör impedanciája

\(\displaystyle Z=\sqrt{R^2+\frac{1}{\left(1/(L\omega)-\omega C\right)^2}},\)

vagyis az ellenálláson átfolyó áram amplitúdója:

\(\displaystyle I_0=U_0\frac{\vert1-LC\omega^2\vert}{\sqrt{R^2(1-LC\omega^2)^2+\omega^2L^2}}\)

\(\displaystyle b)\) Az ellenálláson \(\displaystyle L\omega=\frac1{\omega C}\), vagyis rezonancia esetén nem folyik áram.

II. megoldás A feladat szemléletesen megoldható forgóvektorok (fazorok, amplitúdót és fázist kifejező vektorok) segítségével is.

Vegyük fel először a párhuzamosan kapcsolt tekercs és kondenzátor \(\displaystyle U_{\mathrm{L}}=U_{\mathrm{C}}\) feszültségének megfelelő vektort (vízszintes kék vektor az 1. ábrán).

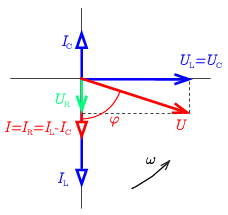
1. ábra

Ezután a tekercs és a kondenzátor áramainak

\(\displaystyle I_{\mathrm{L}}=\frac{U_{\mathrm{L}}}{X_{\mathrm{L}}}=\frac{U_{\mathrm{L}}}{L\omega}\,,\)

illetve

\(\displaystyle I_{\mathrm{C}}=\frac{U_{\mathrm{C}}}{X_{\mathrm{C}}}=U_{\mathrm{L}}\omega C\)

nagyságú vektorát, amelyek a közös feszültséghez képest \(\displaystyle 90^\circ\)-kal késni, illetve sietni fognak.

A főágban és az ellenálláson ennek a két vektornak az eredője fog folyni (\(\displaystyle I_0\), függőleges piros vektor az ábrán, nagysága a két áram nagyságának különbsége), az ellenállás \(\displaystyle U_{\mathrm{R}}=RI_{\mathrm{R}}=RI_0\) feszültsége (zöld vektor) pedig ezzel azonos fázisú, azonos irányba mutat.

Az \(\displaystyle U_0\) kapocsfeszültséget az \(\displaystyle U_{\mathrm{L}}=U_{\mathrm{C}}\) és az \(\displaystyle U_{\mathrm{R}}\) vektorok eredője adja meg.

Az (előző megoldásban is felírt) számítások most már az ábra alapján egyszerűen elvégezhetők:

\(\displaystyle I_0=\left|\frac{U_{\mathrm{L}}}{L\omega}-U_{\mathrm{L}}\omega C\right|=U_{\mathrm{L}}\left|\frac{1}{L\omega}-\omega C\right|\quad\rightarrow\quad U_{\mathrm{L}}=\frac{I_0}{\left|\frac{1}{L\omega}-\omega C\right|}\,,\)

\(\displaystyle U_0=\sqrt{U_{\mathrm{R}}^2+U_{\mathrm{L}}^2}=I_0\sqrt{R^2+\frac{1}{\left(\frac{1}{L\omega}-\omega C\right)^2}}=I_0\frac{\sqrt{R^2\left(1-LC\omega^2\right)^2+\omega^2L^2}}{\left|1-LC\omega^2\right|}\quad\rightarrow\)

\(\displaystyle \rightarrow\quad I_0=U_0\frac{\left|1-LC\omega^2\right|}{\sqrt{R^2\left(1-LC\omega^2\right)^2+\omega^2L^2}}\,,\)

az előző megoldással egyezően.

Az 1. ábrán \(\displaystyle I_{\mathrm{L}}>I_{\mathrm{C}}\), így a főágbeli \(\displaystyle I_0\) áram

\(\displaystyle \varphi=\arccos\frac{U_{\mathrm{R}}}{U_0}=\arccos\frac{R\left|1-LC\omega^2\right|}{\sqrt{R^2\left(1-LC\omega^2\right)^2+\omega^2L^2}}\)

szöggel késni fog az \(\displaystyle U_0\) kapocsfeszültséghez képest.

Ha a körfrekvenciát növeljük, akkor a tekercs árama csökkenni, a kondenzátor árama nőni fog, így a különbségük (\(\displaystyle I_0\)) csökkenni fog, a \(\displaystyle \varphi\) szög pedig egyre nagyobb lesz.

\(\displaystyle \omega=\sqrt{\frac{1}{LC}}=\omega_0\)

körfrekvencia közelében a fázis (az \(\displaystyle I_0\) áram fáziskésése az \(\displaystyle U_0\) kapocsfeszültséghez képest) \(\displaystyle 90^\circ\)-hoz tart.

\(\displaystyle \omega=\omega_0\) körfrekvenciánál az \(\displaystyle I_0\) áram nullává válik, ez a válasz a \(\displaystyle b)\) kérdésre.

Ha a körfrekvenciát kicsit tovább növeljük, akkor már \(\displaystyle I_{\mathrm{L}}<I_{\mathrm{C}}\), a fázis hirtelen előjelet vált, az \(\displaystyle I_0\) áram sietni fog az \(\displaystyle U_0\) kapocsfeszültséghez képest (2. ábra). A körfrekvencia további növelésével az áram nagysága nőni, a fázis abszolút értéke csökkenni fog.

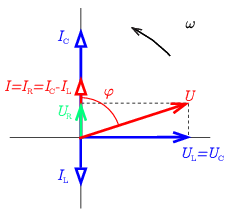
2. ábra

A 3. ábrán az \(\displaystyle I_0\) áram nagyságát ábrázoltuk (\(\displaystyle \tfrac{U_0}{R}\) egységekben), az \(\displaystyle \omega\) körfrekvencia függvényében (\(\displaystyle \omega_0\) egységekben, a vízszintes tengelyen logaritmikus a skála). A két görbét más-más

\(\displaystyle r=R\sqrt{\frac{C}{L}}\)

dimenziótlan paraméter jellemzi. (Érdekes módon ebben a rezgőkörben akkor van éles rezonancia, ha \(\displaystyle R\) nagy.) A grafikonon az \(\displaystyle r=0{,}1\) (kék) és az \(\displaystyle r=1\) (piros) esetet ábrázoltuk.

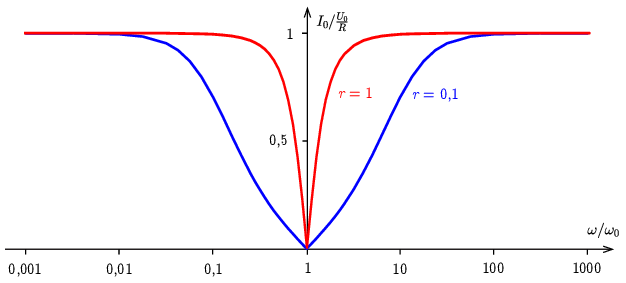
3. ábra

Végül a 4. ábra az áramkör fázisát mutatja, szintén az \(\displaystyle \omega\) körfrekvencia függvényében, két különböző \(\displaystyle r\) érték esetében.

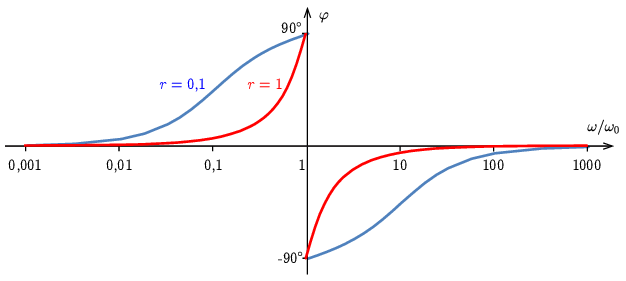
4. ábra

III. megoldás. \(\displaystyle a)\) A feladat a komplex impedanciák módszerével is kezelhető. A kör eredő komplex impedanciája a soros és párhuzamos kapcsolások összefüggéseit felhasználva:

\(\displaystyle Z=R+\frac{1}{(i\omega L)^{-1}+i\omega C}=R+\frac{i\omega L}{1-LC\omega^2}\,.\)

A főágban folyó (komplex) áramerősség innen:

\(\displaystyle I=\frac{U_0}{Z}=\frac{U_0(1-LC\omega^2)}{R(1-LC\omega^2)+i\omega L}\,.\)

Az áram amplitúdója a fenti komplex kifejezés abszolút értékeként számítható:

\(\displaystyle I_0=\frac{U_0\vert 1-LC\omega^2\vert}{\sqrt{R^2(1-LC\omega^2)^2+\omega^2L^2}}\,.\)

\(\displaystyle b)\) Az előző egyenletet vizsgálva észrevehető, hogy amennyiben \(\displaystyle \omega^2LC=1\), akkor a számláló zérussá válik, míg a nevező \(\displaystyle \omega L\) értékű marad. Így a teljes amplitúdó is zérus értékűvé válik, vagyis a kérdéses rezonanciafrekvencia:

\(\displaystyle \omega=\frac{1}{\sqrt{LC}}\,.\)

Statisztika:

31 dolgozat érkezett.
5 pontot kapott:	Bencz Benedek, Bernhardt Dávid, Bogdán Benedek, Bunford Luca, Debreceni Dániel, Fajszi Karsa, Fehérvári Donát, Fekete Lúcia, Kis Márton Tamás, Klement Tamás, Kovács Kristóf , Molnár Kristóf, Seprődi Barnabás Bendegúz, Szabó Donát, Tárnok Ede , Tóth Hanga Katalin, Tóth Kolos Barnabás, Tóthpál-Demeter Márk.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2024. januári fizika feladatai