 |
A P. 5546. feladat (2024. február) |
P. 5546. Az Eszkimók Csodák Palotájában található egy függőleges tengely körül \(\displaystyle \omega=\pi/6~\text{s}^{-1}\) szögsebességgel forgó, \(\displaystyle R=3~\text{m}\) sugarú, kör alakú jégpályára épített iglu. A forgó igluban két gyerek ül az ábrán látható helyzetben, egymáshoz képest \(\displaystyle \varphi=120^\circ\)-os szögben. Az \(\displaystyle A\) pontban ülőnek sikerül úgy elindítania egy kis méretű korongot, hogy az pont a \(\displaystyle B\) helyen ülő társa kezébe érkezzen az indítást követően \(\displaystyle t=2~\text{s}\) múlva.
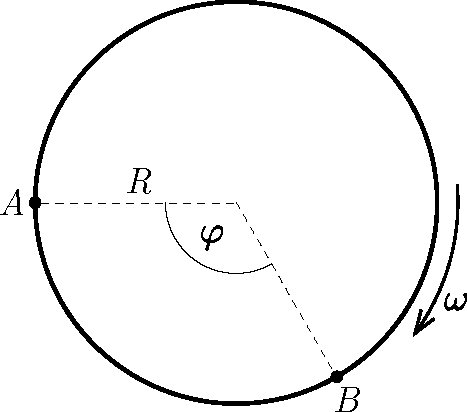
\(\displaystyle a)\) Az igluhoz képest mekkora sebességgel és milyen irányba kellett a korongot az \(\displaystyle A\) pontban ülő gyermeknek ellöknie?
\(\displaystyle b)\) Mekkora távolságra közelíti meg a korong a mozgása során az iglu középpontját?
Közli: Szász Krisztián, Budapest
(5 pont)
A beküldési határidő 2024. március 18-án LEJÁRT.
Megoldás. \(\displaystyle a)\) Az iglu \(\displaystyle t=2\,\mathrm{s}\) idő alatt \(\displaystyle \alpha=\omega t=60^\circ\)-ot fordul el, tehát (az inerciarendszerből nézve) a \(\displaystyle B\) pont a \(\displaystyle B'\) pontba kerül. A korong – súrlódás hiányában – az inerciarendszerben egyenes vonalú egyenletes mozgást végez, és \(\displaystyle t\) idő alatt a \(\displaystyle \overline{AB'}=R\) távolságot kell megtennie (\(\displaystyle \varphi-\alpha=60^\circ\)). Eszerint a sebesség nagysága az inerciarendszerből nézve
\(\displaystyle v_\mathrm{ir}=\frac{R}{t}=1{,}5\,\mathrm{m/s},\)
iránya pedig az \(\displaystyle A\) ponthoz húzott sugárral \(\displaystyle 60^\circ\)-os szöget zár be (1. ábra).
1. ábra
Az inerciarendszerből nézve az \(\displaystyle A\) pont \(\displaystyle v_A=R\omega=\pi/2\,\mathrm{m/s}\) sebességgel mozog, az ellökés pillanatában a rajzon függőlegesen felfelé. A korong sebességvektora az igluból nézve
\(\displaystyle \boldsymbol{v}=\boldsymbol{v}_\mathrm{ir}-\boldsymbol{v}_A.\)
2. ábra
A sebességvektor nagysága a koszinusztétel alapján (2. ábra):
\(\displaystyle v=\sqrt{v_\mathrm{ir}^2+v_A^2-2v_\mathrm{ir}v_A\cos150^\circ}=2{,}97\,\mathrm{m/s},\)
az \(\displaystyle A\) ponthoz húzott sugárral bezárt \(\displaystyle \beta\) szöge pedig a szinusztétel alapján:
\(\displaystyle \frac{\sin(90^\circ-\beta)}{\sin150^\circ}=\frac{v_\mathrm{ir}}{v}\qquad\rightarrow\qquad\beta=75{,}4^\circ.\)
\(\displaystyle b)\) A korong az iglu középpontjához legközelebb a mozgása felénél lesz. A pont középponttól mért távolsága ugyanakkora az igluból és az inerciarendszerből nézve is. A távolság könnyen leolvasható az 1. ábráról, ami az \(\displaystyle R\) oldalú szabályos háromszög magassága:
\(\displaystyle d_\mathrm{min}=\frac{\sqrt{3}}{2}R=2{,}6\,\mathrm{m}.\)
Megjegyzés. Nem része a feladatnak, de számítógéppel kirajzolható a pályagörbe az igluból nézve (a korong iglu jegén hagyott nyoma). Ha felveszünk egy derékszögű koordináta-rendszert, melynek középpontja az iglu középpontja, és az \(\displaystyle A\) pont koordinátái (\(\displaystyle -R\) , 0), akkor az inerciarendszerben könnyen felírhatjuk a korong koordinátáit az idő függvényében:
$$\begin{align*} x_\mathrm{ir}&=-R+\frac{v_\mathrm{ir}}{2}t,\\ y_\mathrm{ir}&=\frac{-\sqrt{3}v_\mathrm{ir}}{2}t. \end{align*}$$Az iglu állandó \(\displaystyle -\omega\) szögsebességgel elfordul az inerciarendszerhez képest, így az igluból nézve az inerciarendszer forog \(\displaystyle \omega\) szögsebességgel. Az igluhoz rögzített koordináta-rendszerben (amely az ellökés pillanatában megegyezik az inerciarendszerbelivel) a \(\displaystyle t\) időpillanatban egy \(\displaystyle \omega t\) szögű forgatással kapjuk meg a korong koordinátáit:
$$\begin{align*} x&=x_\mathrm{ir}\cos(\omega t)-y_\mathrm{ir}\sin(\omega t)=\left(-R+\frac{v_\mathrm{ir}}{2}t\right)\cos(\omega t)+\frac{\sqrt{3}v_\mathrm{ir}}{2}t\sin(\omega t),\\ y&=x_\mathrm{ir}\sin(\omega t)+y_\mathrm{ir}\cos(\omega t)=\left(-R+\frac{v_\mathrm{ir}}{2}t\right)\sin(\omega t)-\frac{\sqrt{3}v_\mathrm{ir}}{2}t\cos(\omega t). \end{align*}$$Az (\(\displaystyle x\) , \(\displaystyle y\)) pontok ezután már sokféle programmal könnyen ábrázolhatók (3. ábra).
3. ábra
Statisztika:
47 dolgozat érkezett. 5 pontot kapott: Barna Márton, Bencze Mátyás, Csiszár András, Czirják Márton Pál, Fehérvári Donát, Gerendás Roland, Gyenes Károly, Hegedüs Márk, Masa Barnabás, Seprődi Barnabás Bendegúz, Sütő Áron, Szabó Donát, Tóth Hanga Katalin, Zólomy Csanád Zsolt. 4 pontot kapott: Bernhardt Dávid, Csapó András, Csóka Péter, Erős Fanni, Fajszi Karsa, Monok Péter, Tóth Kolos Barnabás. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 8 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2024. februári fizika feladatai