A P. 5549. feladat (2024. február)

P. 5549. Homogén tömegeloszlású, $\displaystyle M$ tömegű, vékony huzalból zárt síkgörbét hajlítunk. Az így kapott keret tehetetlenségi nyomatéka a tömegközéppontján áthaladó, síkjára merőleges tengelyre vonatkozóan $\displaystyle \Theta_0$. A testtel ezután kísérletet végzünk az ábrán vázolt módon: különböző pontjai mentén felfüggesztjük, majd mérjük a kis amplitúdójú, saját síkjába eső lengéseinek periódusidejét. Mekkora a lehetséges legkisebb lengésidő?

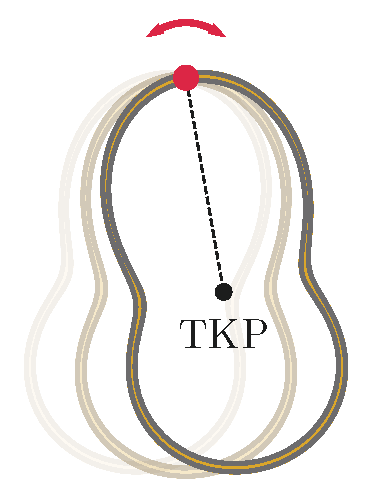
Dürer Verseny feladata nyomán

(5 pont)

A beküldési határidő 2024. március 18-án LEJÁRT.

Megoldás. Tekintsünk egy tetszőleges felfüggesztési pontot, jelölje ennek a keret tömegközéppontjától mért távolságát $\displaystyle s$, a test erre vonatkozó tehetetlenségi nyomatékát $\displaystyle \Theta_s$. Utóbbi kapcsolatba hozható a tömegközépponti tehetetlenségi nyomatékkal a $\displaystyle \Theta_s=\Theta_0+Ms^2$ Steiner-tétel által. Ezt felhasználva, a kiválasztott tengelyhez tartozó lengésidő az alábbi alakot ölti:

A gyök alatti kifejezés alulról becsülhető a számtani és mértani közepek közötti egyenlőtlenség segítségével:

$\displaystyle \frac{\Theta_0}{Mgs}+\frac{s}{g}\ge\sqrt{\frac{4\Theta_0}{Mg^2}}.$

Egyenlőség akkor lép fel, amikor a két tag megegyezik; ez a feltétel az alábbi speciális $\displaystyle s_\mathrm{min}$ érték esetén teljesül, amelyet az 1. ábrán is vázoltunk:

$\displaystyle s_\mathrm{min}=\sqrt{\frac{\Theta_0}{M}}.$

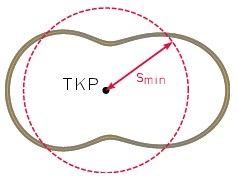
1. ábra

Kérdés, hogy van-e olyan pontja a keretnek, amely a tömegközépponttól éppen ekkora távolságra esik. Hogy ezt megválaszoljuk, érdemes a tehetetlenségi nyomaték definícióját felhasználva $\displaystyle s_\mathrm{min}$ négyzetét szemléletesebb alakra hozni:

azaz $\displaystyle s_\mathrm{min}$ éppen a huzal egyes pontjaihoz tartozó $\displaystyle s$ távolságok négyzetes közepe. Mivel a középérték biztosan a legkisebb és legnagyobb távolságok közé esik, a huzal folytonossága miatt annak biztosan lesz legalább egy pontja, amely $\displaystyle s_\mathrm{min}$ távol helyezkedik el a tömegközépponttól. Az ehhez tartozó minimális $\displaystyle T_\mathrm{min}$ lengésidő az (1) egyenlethez visszatérve kiszámítható:

$\displaystyle T_\mathrm{min}=2\pi\sqrt[4]{\frac{4\Theta_0}{Mg^2}}.$

Végeredményben tehát ez lesz a mért lengésidők minimuma.

Megjegyzés. Érdekesség, hogy a (2) egyenletből nem csupán az következik, hogy a huroknak legalább egy pontja a tömegközépponttól $\displaystyle s_\mathrm{min}$ távolságra esik, hanem az is, hogy legalább kettő. Ennek oka, hogy a hurok zárt, így bármely metszésponthoz, ahol a huzal az 1. ábrán jelölt körbe belép, kell tartoznia egy másik pontnak is, ahol kilép. Egyetlen érintési pont nem jöhet létre, hiszen a huzal nem lehet teljes egészében sem a körön belül, sem azon kívül. A két minimális lengésidejű pont esetére konstrukció is adható, például a 2. ábrán látható patkószerű hurok.

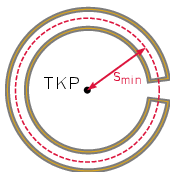
2. ábra

Statisztika:

32 dolgozat érkezett.
5 pontot kapott:	Czirják Márton Pál, Gyenes Károly, Pázmándi József Áron.
4 pontot kapott:	Bencz Benedek, Bernhardt Dávid, Csiszár András, Csóka Péter, Debreceni Dániel, Dobos Anita, Fajszi Karsa, Fehérvári Donát, Gerendás Roland, Kiss 131 Adorján Timon, Klement Tamás, Masa Barnabás, Nguyen Kim Dorka, Simon János Dániel, Sütő Áron, Szabó Donát, Tóth Hanga Katalin, Tóth Kolos Barnabás.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2024. februári fizika feladatai