 |
A P. 5550. feladat (2024. február) |
P. 5550. Lézerfénnyel megvilágítjuk az \(\displaystyle R\) sugarú, \(\displaystyle n\) törésmutatójú gömblencsét. Merre kell irányítani az optikai tengelyen a lencse középpontjától \(\displaystyle d\) távolságra lévő pontból kiinduló fénysugarat, hogy az a lencsén megtörve a lencse másik oldalán a középponttól ugyancsak \(\displaystyle d\) távolságra metssze az optikai tengelyt? Adott törésmutató mellett milyen \(\displaystyle d\) estén lehetséges ez a fénysugármenet? Számoljuk ki a kérdéses irány szögét a \(\displaystyle {d=2R}\), \(\displaystyle {n=3/2}\) adatokkal!
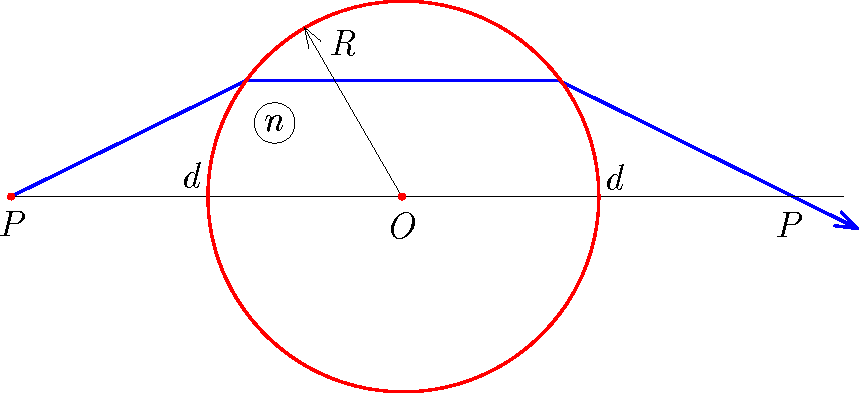
Közli: Cserti József, Budapest
(4 pont)
A beküldési határidő 2024. március 18-án LEJÁRT.
Megoldás. Jelöljük \(\displaystyle A\)-val azt a pontot, ahol a sugár a gömblencsébe belép, \(\displaystyle s\)-sel az \(\displaystyle \overline{AP}\) szakasz hosszát, a beesési és a törési szög pedig legyen rendre \(\displaystyle \alpha\) és \(\displaystyle \beta\).
Az \(\displaystyle OAP\) háromszögre felírható szinusz tétel és a töréstörvény szerint
\(\displaystyle \frac{d}{s}=\frac{\sin(180^\circ -\alpha)}{\sin \beta}=n,\)
azaz
\(\displaystyle s=\frac{d}{n}.\)
A \(\displaystyle \beta\) valamint az \(\displaystyle \alpha-\beta\) szögekre felírható koszinusz tételnek megfelelően
\(\displaystyle s^2=R^2+d^2-2Rd\cos\beta,\)
illetve
\(\displaystyle R^2=s^2+d^2-2sd\cos(\alpha-\beta).\)
Ezekbe \(\displaystyle s\)-t behelyettesítve némi átrendezés után kapjuk, hogy
\(\displaystyle \cos\beta=\frac{d}{2 R}\,\left[1-\frac{1}{n^2}+{\left(\frac{R}{d}\right)}^2\right],\)
és
\(\displaystyle \cos\left(\alpha-\beta\right)=\frac{1}{2n}+\frac{n}{2}\,\left[1-{\left(\frac{R}{d}\right)}^2 \right].\)
Az elrendezésből adódóan természetes, hogy \(\displaystyle d>R\), és az egyenleteknek csak akkor értelmezhető a megoldása, ha \(\displaystyle 1\geq\cos\beta\geq 0\), illetve \(\displaystyle 1\geq\cos\left(\alpha-\beta\right)\geq 0\) adódik. Egyszerűen látható, ha \(\displaystyle d>R\), mindkét koszinusz pozitív. A
\(\displaystyle (\cos\beta=)\,\frac{d}{2 R}\,\left[1-\frac{1}{n^2}+{\left(\frac{R}{d}\right)}^2\right]\leq 1\)
feltétel azonos átalakításokkal az
\(\displaystyle \frac{R}{d}\geq 1-\frac{1}{n}\)
egyenlőtlenségre vezet, de ugyanezt kapjuk, ha a \(\displaystyle 1\geq\cos\left(\alpha-\beta\right)\) feltételből indulunk ki. Tehát a kérdésben szereplő sugármenet csak akkor lehetséges, ha
| \(\displaystyle (5)\) | \(\displaystyle R<d\leq\frac{nR}{n-1}.\) |
A feladatban szereplő \(\displaystyle d=2R\), \(\displaystyle n=3/2\) adatokkal:
$$\begin{align*} \cos\beta &=\frac{29}{36}\quad\to\quad\beta=36{,}4^\circ,\\ \cos\left(\alpha-\beta\right)&=\frac{43}{48}\quad\to\quad\alpha-\beta=26{,}4^\circ. \end{align*}$$Megjegyzés. A vastag lencsékről, amely kategóriába egy gömblencse is tartozik, lapunk 1967. évi 8-9. számában olvashatunk bővebben (Dr. Vermes Miklós, A vastag lencsék, Középiskolai Matematikai Lapok, 35. kötet 3-4. szám). Eszerint az (5) egyenlőtlenség jobb oldalán álló kifejezés pontosan a gömblencse \(\displaystyle f=nR/2(n-1)\) fókusztávolságának a kétszerese. Fontos észrevétel, hogy egy ,,általános" \(\displaystyle d<2f\) esetben a leképezési törvény szerint a \(\displaystyle P\) pont képe a kétszeres fókusztávolságon kívül keletkezik. Ezzel nincs összhangban a vizsgált sugármenet. Az ellentmondás oka, hogy a leképezési törvény csak az optikai tengelyhez közel haladó sugarakat veszi figyelembe, de ez a sugár nem ilyen.
Statisztika:
18 dolgozat érkezett. 3 pontot kapott: Bogdán Benedek, Bunford Luca, Csernyik Péter, Fekete Lúcia, Gyenes Károly, Kátai Ferdinánd, Kis Márton Tamás, Kovács Kristóf , Molnár Kristóf, Nguyen Kim Dorka. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2024. februári fizika feladatai