 |
A P. 5555. feladat (2024. március) |
P. 5555. Vízszintes, nem teljesen sima asztallapon nyugszik egy r sugarú korong. A síkon egy nagyobb, R=2r sugarú korong forgásmentesen csúszik úgy, hogy a középpontja a kis korong érintője mentén mozog. Mindkét korong ugyanabból az anyagból készült és a magasságuk is ugyanakkora.
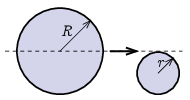
A rugalmasnak tekinthető ütközés után a nagy korong a súrlódás miatt lelassul és d=5 cm út megtétele után megáll. Milyen irányban és milyen messzire jut el a kis korong az asztalon? A korongok közötti súrlódás elhanyagolható.
Közli: Holics László, Budapest
(4 pont)
A beküldési határidő 2024. április 15-én LEJÁRT.
Megoldás. Az ütközés nagyon rövid ideje alatt a külső erők (az asztallap és a korongok közötti súrlódás) hatása figyelmen kívül hagyható, vagyis a két korongból álló rendszer zártnak tekinthető. Az ütközés során a teljes mozgásmennyiség (impulzus) vektora állandó marad. Az ütközés rugalmas, így a korongok összes mozgási energiája sem változik meg. A korongok közötti súrlódás elhanyagolható, emiatt a korongok nem jöhetnek forgásba, vagyis a mozgási energia tisztán a transzlációs mozgásból származik.
Jelöljük a nagyobb korong ütközés előtti sebességvektorát \displaystyle \boldsymbol{v}_0-lal. Ha a kis korong tömege \displaystyle m, akkor a megadott feltételek miatt a nagyobb korong tömege nyilván \displaystyle 4m lesz. Az ütközés pillanatában (lásd az 1. ábrát) a korongok \displaystyle P és \displaystyle Q középpontjára illeszkedő egyenesnek a nagyobb korong kezdeti mozgásirányával bezárt szöge:
| \displaystyle (1) | \displaystyle \varphi=\arcsin\frac{r}{R+r}=\arcsin\frac{1}{3}=19{,}5^\circ. |

1. ábra
Az ütközés során a két korong között egy nagyon rövid ideig tartó, nagyon nagy \displaystyle \boldsymbol{F}(t) erő lép fel, ami a kezdetben álló kis korongot \displaystyle P\rightarrow Q irányba valamekkora \displaystyle \boldsymbol{u} sebességgel meglöki. Eközben a nagy korong sebessége \displaystyle \boldsymbol{v}-re változik (2. ábra). A kis korong az ütközés előtt állt, így \displaystyle \boldsymbol{u} iránya nyilván megegyezik \displaystyle \boldsymbol{F} irányával.

2. ábra
Az ábrán látható koordináta-rendszerben az impulzusmegmaradás törvénye szerint
\displaystyle 4mv_0=4mv_x+mu\cos\varphi,
\displaystyle 0=4mv_y-mu\sin\varphi,
vagyis
| \displaystyle (2) | \displaystyle v_x=v_0-\frac{u\cos\varphi}{4}, |
| \displaystyle (3) | \displaystyle v_y=-\frac{u\sin\varphi}{4}. |
Az energiamegmaradás törvényét alkalmazva felírhatjuk, hogy
| \displaystyle (4) | \displaystyle \frac{1}{2}(4m)v_0^2=\frac{1}{2}(4m)\left(v_x^2+v_y^2\right)+\frac{1}{2}mu^2. |
(2)-t és (3)-t (4)-be helyettesítve az \displaystyle u sebességnagyságra egy hiányos másodfokú egyenletet kapunk, aminek az egyik (számunkra érdektelen) megoldása \displaystyle u=0, a másik gyöke pedig
| \displaystyle (5) | \displaystyle u=\frac{8}{5}v_0\cos\varphi=1{,}51\,v_0. |
(2), (3) és (5) felhasználásával a korongok sebességkomponensei:
\displaystyle u_x=u\cos\varphi=1{,}42\,v_0,
\displaystyle u_y=-u\sin\varphi=-0{,}50\,v_0,
\displaystyle v_x=0{,}64\,v_0,
\displaystyle v_y=0{,}13\,v_0.
Az ütközés után a nagy korong sebességnagyságának négyzete:
\displaystyle v^2=v_x^2+v_y^2=0{,}43\,v_0^2,
a kis korongé pedig
\displaystyle u^2=u_x^2+u_y^2=2{,}28\,v_0^2.
Az asztallapon csúszó korongok az asztallal való súrlódásuk miatt ugyanolyan ütemben egyenletesen lassulva mozognak, a megállásukig megtett útjuk a kezdősebességük négyzetével arányos. Ennek megfelelően a kisebb korong
\displaystyle d=\frac{u^2}{v^2}\cdot \text{5 cm}=26{,}5\,\mathrm{cm}
út megtétele után áll meg.
A nagy korong az eredeti mozgásirányához képes
\displaystyle \alpha=\arctg\frac{v_y}{v_x}=11{,}1^\circ
szögben ,,balra'' térül el, a kis korong elmozdulásának iránya pedig ,,jobbra''
\displaystyle \beta=\arctg\frac{\vert u_y\vert}{u_x}=\varphi=19{,}5^\circ
a nagyobb korong kezdeti mozgásirányához viszonyítva.
Statisztika:
30 dolgozat érkezett. 4 pontot kapott: Bélteki Teó, Csapó András, Csiszár András, Csóka Péter, Czirják Márton Pál, Dobos Anita, Gyerő Soma, Hegedüs Márk, Szabó Donát, Zádori Gellért, Zólomy Csanád Zsolt. 3 pontot kapott: Hornok Máté, Kiss 131 Adorján Timon, Magyar Zsófia, Sütő Áron, Vágó Botond. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2024. márciusi fizika feladatai
|
|

