A P. 5558. feladat (2024. március)

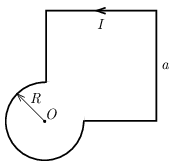
P. 5558. Az ábrán látható háromnegyed kör sugara $\displaystyle R$, a hiányos négyzet oldalainak hosszúsága $\displaystyle a$. A zárt vezető körben $\displaystyle I$ erősségű áram folyik. Határozzuk meg a mágneses indukcióvektor értékét a kör $\displaystyle O$ középpontjában!

Útmutatás: Egy $\displaystyle \ell$ oldalhosszúságú, $\displaystyle I$ árammal átjárt, négyzet alakú vezetőkeret középpontjában a mágneses indukció értéke:

$\displaystyle B=\frac{2\sqrt{2}\mu_0I}{\pi\ell}.$

Közli: Kotek László, Pécs

(4 pont)

A beküldési határidő 2024. április 15-én LEJÁRT.

Megoldás. Az eredő $\displaystyle \boldsymbol{B}$ mágneses indukció a háromnegyed kör $\displaystyle \boldsymbol{B}_1$ és a hiányos négyzet $\displaystyle \boldsymbol{B}_2$ járulékának összege. Mindkét vektor az ábra síkjára merőleges és abból kifelé mutat, így az eredő mágneses indukció nagysága: $\displaystyle B=B_1+B_2$.

A hiányos négyzet azon oldalai, amelyek meghosszabbítása áthalad $\displaystyle O$-n, a Biot–Savart-törvény szerint nem járulnak hozzá a mágneses indukció $\displaystyle O$ pontbeli értékéhez.

Ismert, hogy egy $\displaystyle R$ sugarú körvezető középpontjában a mágneses indukcióvektor nagysága $\displaystyle \frac{\mu_0I}{2R}$. Ezek szerint a háromnegyed kör mentén folyó, $\displaystyle I$ erősségű áram a kör középpontjában $\displaystyle B_1=\frac{3\mu_0I}{8R}$ nagyságú mágneses indukciót hoz létre.

Tekintsünk egy $\displaystyle \ell=2a$ oldalélű négyzetet, amely oldalai mentén $\displaystyle I$ erősségű áram folyik. A mágneses indukcióvektor nagysága a négyzet $\displaystyle O$ középpontjában $\displaystyle B_0=\frac{2\sqrt{2}\mu_0I}{2\pi a}$. A feladatunkban szereplő két oldalél a teljes négyzetnek csak az egynegyede, így a járulékuk:

$\displaystyle B_2=\frac{B_0}{4}=\frac{\sqrt{2}\mu_0I}{4\pi a}.$

A teljes mágneses indukcióvektor nagysága ezek szerint

$\displaystyle B=\mu_0I\left(\frac{3}{8R}+ \frac{\sqrt{2}}{4\pi a}\right).$

Statisztika:

25 dolgozat érkezett.
4 pontot kapott:	Barna Márton, Bencze Mátyás, Csernyik Péter, Csiszár András, Csóka Péter, Dobos Anita, Fekete Lúcia, Gerendás Roland, Gyenes Károly, Klement Tamás, Pázmándi József Áron, Seprődi Barnabás Bendegúz, Szabó Donát.
3 pontot kapott:	Bélteki Teó, Csapó András, Erős Fanni, Gyerő Soma, Kátai Ferdinánd, Masa Barnabás, Molnár Kristóf.
1 pontot kapott:	1 versenyző.

A KöMaL 2024. márciusi fizika feladatai