 |
A P. 5559. feladat (2024. március) |
P. 5559. Kis nyílásszögű, \(\displaystyle R\) sugarú homorú és domború gömbtükröket az ábrán látható módon helyezünk el egymástól \(\displaystyle 1{,}25 R\) távolságra.
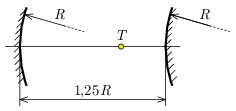
A közös optikai tengely mely \(\displaystyle T\) pontjába helyezzünk egy pontszerű fényforrást, hogy a belőle induló fénysugarak a két tükörről való visszaverődés után a \(\displaystyle T\) ponton menjenek át?
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2024. április 15-én LEJÁRT.
Megoldás. Az egyszerű gömbtükrök fókusztávolsága \(\displaystyle f=\pm R/2\), így az adott elrendezésben a két eszköz távolsága éppen \(\displaystyle D=2{,}5f\). Legyen a \(\displaystyle T\) pont távolsága a homorú tükörtől \(\displaystyle t\)! A \(\displaystyle T\) pontról a homorú tükörtől
\(\displaystyle k=\frac{tf}{t-f}\)
távolságra keletkezne kép, de ez csak a domború tükör mögött lehetne (másképp a domború tükrön való visszaverődés után nem találkozhatnának a fénysugarak). Ez a kép tehát virtuális tárgyat jelent a domború tükör számára, amely a tükör mögött \(\displaystyle t_v=k-D\) távolságra van. Erről a domború tükör előtt \(\displaystyle D-t\) távolságra keletkezik egy valódi kép, tehát
\(\displaystyle -\frac{1}{f}=\frac{1}{D-t}-\frac{1}{k-D}.\)
A két egyenletből \(\displaystyle k\) kiküszöbölésével a
\(\displaystyle t^2-t(2f+D)+f(2f+D)=0\)
másodfokú egyenletet kapjuk, aminek a gyökei
\(\displaystyle t=\frac{(2f+D)\pm\sqrt{D^2-(2f)^2}}{2}.\)
Ezek közül a negatív előjelet tartalmazó kisebb, míg a másik nagyobb mint \(\displaystyle D\), tehát a keresett érték
\(\displaystyle t=\frac{(2f+D)-\sqrt{D^2-(2f)^2}}{2}=\frac{3}{2}f=\frac{3}{4}R.\)
Megjegyzések. 1. A fenti leírás a \(\displaystyle T\) pontból a homorú tükör felé induló kicsiny nyílásszögű sugárnyalábot követte, de nyilván ugyanezt kapjuk, ha a domború tükör felé induló sugarakat nézzük: azok ugyanezt az utat futják be, csak ellenkező irányban.
2. A gyökök és együtthatók összefüggése alapján a másodfokú egyenlet két gyökére igaz, hogy
\(\displaystyle t_1+t_2=2f+D\qquad\textrm{és}\qquad t_1\cdot t_2=f(2f+D).\)
A két egyenletet elosztva egymással azt találjuk, hogy
\(\displaystyle \frac{1}{t_1}+\frac{1}{t_2}=\frac{1}{f}.\)
Ha tehát mondjuk \(\displaystyle t_1=t\), akkor \(\displaystyle t_2=k\).
Statisztika:
24 dolgozat érkezett. 5 pontot kapott: Csapó András, Csóka Péter, Czirják Márton Pál, Debreceni Dániel, Dobos Anita, Fehérvári Donát, Fekete Lúcia, Gyenes Károly, Hegedüs Márk, Klement Tamás, Molnár Kristóf, Szabó Donát, Tóthpál-Demeter Márk, Žigo Boglárka. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2024. márciusi fizika feladatai
