 |
A P. 5561. feladat (2024. március) |
P. 5561. Egy két végén rögzített, hosszegységenként \(\displaystyle \mu\) tömegű, \(\displaystyle 2L\) hosszúságú megfeszített húron a transzverzális hullámok terjedési sebessége \(\displaystyle c\).
\(\displaystyle a)\) Adjuk meg a húr sajátrezgéseinek lehetséges frekvenciáit \(\displaystyle c/L\) egységekben!
\(\displaystyle b)\) A húr közepére egy \(\displaystyle M=2\mu L\) tömegű, pontszerű testet rögzítünk, ahogy az az ábrán látható. Írjunk fel egy egyenletet a húr sajátrezgéseinek lehetséges frekvenciáira, és számítsuk is ki a legalacsonyabb 3 frekvencia számszerű értékét \(\displaystyle c/L\) egységekben! A gravitáció hatása elhanyagolható.
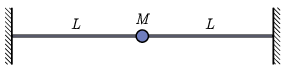
Útmutatás: Belátható, hogy a hullámalakok a középpontra nézve páros vagy páratlan függvényekkel írhatóak le.
Közli: Vigh Máté, Biatorbágy
(6 pont)
A beküldési határidő 2024. április 15-én LEJÁRT.
Megoldás. \(\displaystyle a)\) A húron állóhullámok alakulnak ki, melyek lehetséges \(\displaystyle \lambda_n\) hullámhosszait a rögzített végek miatt a következő feltétel határozza meg:
\(\displaystyle n\frac{\lambda_n}{2}=2L,\)
ebből \(\displaystyle \lambda_n=4L/n\), ahol \(\displaystyle n=1,2,\ldots\) az alap- és felharmonikusoknak megfelelő pozitív egész számok. A megfelelő frekvenciák a fázissebesség segítségével így írhatók:
\(\displaystyle f_n=\frac{c}{\lambda_n}=\frac{n}{4}\frac{c}{L}.\)
\(\displaystyle b)\) Mivel most is sajátrezgéseket keresünk (azaz olyan mozgásformát, melyben a húr minden pontja és az \(\displaystyle M\) tömegű test is azonos frekvenciával, azonos vagy ellentétes fázisban mozog), a húr két felén egyforma hullámhosszú állóhullám fog kialakulni. Két lehetőség van: a húr két fele vagy azonos fázisban rezeg (ez a középpontra nézve páros függvénnyel írható le) vagy ellentétes fázisban (páratlan függvény). Utóbbi esetben a húr közepének (és így az \(\displaystyle M\) tömegű testnek) a kitérése nulla, ezért ekkor a hullámhosszt meghatározó egyenlet:
\(\displaystyle n\frac{\lambda_n}{2}=L,\qquad\textrm{ahonnan}\qquad f_n=\frac{n}{2}\frac{c}{L}.\)
Itt továbbra is \(\displaystyle n=1,2,\ldots\) egész számok.
A tengelyesen szimmetrikus (páros) megoldásokhoz tartozó sajátfrekvenciák meghatározása egy kicsit nehezebb, melynek oka, hogy a húr közepén a peremfeltétel nem olyan egyszerű, mint rögzített vagy szabad végpont esetében. Válasszunk olyan koordináta-rendszert, melynek origója a húr bal oldali rögzített végpontjában helyezkedik el (\(\displaystyle x=0\)), a pontszerű test vízszintes koordinátája pedig \(\displaystyle x=L\). A húr bal felén kialakuló transzverzális állóhullám
\(\displaystyle y(x,t)=A\sin(kx)\cos(\omega t)\)
alakban írható fel, hiszen az \(\displaystyle x=0\) helyen rögzített végpont kitérése minden időpillanatban szükségszerűen nulla. Ebben az egyenletben \(\displaystyle k=2\pi/\lambda\) a hullámszám és \(\displaystyle \omega=2\pi f\) a körfrekvencia. A húr gyorsulása az \(\displaystyle x=L\) helyen megegyezik az \(\displaystyle M\) tömegű test \(\displaystyle a\) gyorsulásával:
\(\displaystyle a=\left.\frac{\partial^2y}{\partial t^2}\right\vert_{x=L}=-A\omega^2\sin(kL)\cos(\omega t).\)
A pontszerű test rezgőmozgásának dinamikai feltételét a húrt feszítő \(\displaystyle F\) erő függőleges komponenséből származó eredő erő biztosítja:
\(\displaystyle -2F\sin\alpha=Ma,\)
ahol \(\displaystyle \sin\alpha\) kis kitérések esetén közelíthető a húr érintőjének meredekségével az \(\displaystyle x=L\) helyen:
\(\displaystyle \sin \alpha\approx\tg \alpha =\left.\frac{\partial y}{\partial x}\right\vert_{x=L}=Ak\cos(kL)\cos(\omega t).\)
Az utóbbi három összefüggés felhasználásával a következőt kapjuk:
\(\displaystyle 2FAk\cos(kL)=MA\omega^2\sin(kL).\)
Használjuk fel a húrt feszítő erő és a fázissebesség között fennálló \(\displaystyle c=\sqrt{F/\mu}\) összefüggést, valamint a feladatban megadott \(\displaystyle M=2\mu L\) tömegértéket! Egyszerűsítés és rendezés után kapjuk a
\(\displaystyle c^2k=L\omega^2\tg(kL)\)
egyenletet, ami az \(\displaystyle \omega=ck\) formula segítségével elegáns alakba írható:
\(\displaystyle kL\tg(kL)=1.\)
Ennek a transzcendens egyenletnek a gyökei határozzák meg a lehetséges \(\displaystyle k\) hullámszámokat és az annak megfelelő sajátfrekvenciákat. A gyökök numerikusan (pl. zsebszámológéppel) vagy számítógéppel kereshetők meg, az első három pozitív megoldás:
\(\displaystyle kL=0{,}860\quad 3{,}426\quad 6{,}437\quad\ldots\)
A megfelelő frekvenciák a hullámszám lehetséges értékeinek ismeretében így számolhatók:
\(\displaystyle f=\frac{\omega}{2\pi}=\frac{ck}{2\pi}.\)
A tengelyesen szimmetrikus hullámformákhoz tartozó sajátfrekvenciák tehát:
\(\displaystyle f=0{,}136\frac{c}{L},\quad 0{,}545 \frac{c}{L},\quad 1{,}024\frac{c}{L}\,\quad\ldots\)
A feladat a három legalacsonyabb frekvenciát kérdezte, ezek közül kettő a páros megoldásokhoz, egy pedig a páratlanhoz tartozik:
\(\displaystyle f=0{,}136\frac{c}{L},\quad 0{,}500\frac{c}{L},\quad 0{,}545\frac{c}{L}.\)
Statisztika:
3 dolgozat érkezett. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2024. márciusi fizika feladatai