 Problem P. 5565. (April 2024)
Problem P. 5565. (April 2024)
P. 5565. One end of a long, flexible, heavy chain was fixed. The hanging chain would break if a load greater than the weight of the chain was hung on it. The chain is released from the position shown in the figure. (Both the moving and the already taut parts of the chain can be considered to be vertical.) Will the chain break?
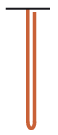
(5 pont)
Deadline expired on May 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Legyen a lánc tömege \(\displaystyle m\), a hossza \(\displaystyle \ell\). Tekintsük azt a helyzetet, amelynél a lánc szabad vége \(\displaystyle x\) távolságra került a rögzített láncvégtől. A lánc mozgásban lévő része ekkor \(\displaystyle \frac{\ell-x}{2}\), az álló része pedig \(\displaystyle \frac{\ell+x}{2}\) hosszúságú. A mozgásban lévő rész szabadon esik, benne nem ébred feszítőerő.
A szabadon eső láncdarab elmozdulása \(\displaystyle t\) idő alatt
| \(\displaystyle (1)\) | \(\displaystyle x(t)=\frac{g}{2}t^2,\) |
sebessége pedig
| \(\displaystyle (2)\) | \(\displaystyle v(t)=gt=\sqrt{2gx(t)}.\) |
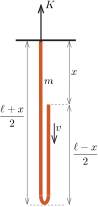
A láncot feszítő erő a jobb oldali részben nulla, a bal oldali (már megfeszült) láncdarabban pedig a felfüggesztési ponttól mért távolsággal arányosan csökken. (Ez az álló láncdarabra felírható erőegyensúly egyenletéből következik.) A feszítőerő tehát a bal oldali láncdarab felső végénél a legnagyobb. Jelöljük ezt az erőt (amelyet a mennyezet fejt ki a láncra) \(\displaystyle K\)-val. Amennyiben a mozgás teljes ideje alatt \(\displaystyle K\le 2mg\), akkor a lánc nem fog elszakadni.
Számítsuk ki, hogy mekkora a lánc \(\displaystyle I\) impulzusa \(\displaystyle t\) idővel az elengedés után. Ennek a mennyiségnek időegységenkénti megváltozása, vagyis az \(\displaystyle I'(t)\) derivált a láncra ható külső erők eredőjével (\(\displaystyle K\) és az \(\displaystyle mg\) nehézségi erő előjeles összegével) egyezik meg.
Mivel a láncdarab tömege a hosszával arányos, a mozgásban lévő rész impulzusa
\(\displaystyle I(t)=\frac{m}{\ell}\cdot \frac{\ell-x(t)}{2}\cdot v(t),\)
vagyis (1) és (2) behelyettesítésével
\(\displaystyle I(t)=\frac{mg}{2}t-\frac{mg^2}{4\ell}t^3.\)
A Newton-féle mozgásegyenlet szerint
\(\displaystyle mg-K(t)=I'(t)=\frac{mg}{2}-\frac{3mg^2}{4\ell}t^2,\)
vagyis
\(\displaystyle K(t)=\frac{mg}{2}+\frac{3mg^2}{4\ell}t^2.\)
A láncot feszítő erő a rögzített végpontjánál indulásakor \(\displaystyle K(0)=\frac{mg}{2}\), az idő múltával \(\displaystyle K(t)\) egyre nagyobb lesz, és a maximális értékét a lánc teljes kiegyenesedésekor, \(\displaystyle T=\sqrt{\frac{2\ell}{g}}\) időpillanatban éri el.
Mivel
\(\displaystyle K(T)=\frac{mg}{2}+\frac{3mg^2}{4\ell}\,\frac{2\ell}{g}=2mg\)
kevesebb, mint a lánc teherbírása, a lánc biztosan nem szakad el.
II. megoldás. Kövessük az I. megoldás jelöléseit! Mialatt az \(\displaystyle x\) távolság egy kicsiny \(\displaystyle \Delta x\) értékkel megnő, a mozgásban lévő láncdarab tömege \(\displaystyle \Delta m=\frac{\Delta x}{2\ell}m\) értékkel változik (csökken). Ekkora tömegű láncdarab sebessége \(\displaystyle v=\sqrt{2gx}\)-ről (rugalmatlan ütközések miatt) nullára csökken, tehát az impulzusváltozása (amit lefelé tekintünk pozitívnak)
\(\displaystyle \Delta I=\Delta m\,v=\frac{mv}{2\ell}\,\Delta x\)
értékkel csökken. Ezt a változást a lánc másik fele által kifejtett
\(\displaystyle K^*=\frac{\Delta I}{\Delta t}\)
nagyságú, felfelé irányuló erő hozza létre. (\(\displaystyle \Delta t=(\Delta x)/v\) a kicsiny láncdarab lefékeződésének ideje.) Így tehát
\(\displaystyle K^*=\frac{mv}{2\ell}\,\frac{\Delta x}{\Delta t}=\frac{mv^2}{2\ell}=mg\,\frac{x}{\ell}.\)
Ennek az erőnek a bal oldali láncdarabra ható ellenereje ugyanekkora nagyságú, de lefelé irányuló erő.
A bal oldali láncdarabra ható erők eredője nulla:
\(\displaystyle K-mg\,\frac{\ell+x}{2\ell}-K^*=0,\)
vagyis
\(\displaystyle K(x)=mg\,\frac{\ell+x}{2\ell}+\frac{x}{\ell}\,mg=\frac{mg}{2}\left(1+3\,\frac{x}{\ell}\right).\)
Mivel
\(\displaystyle x\le\ell, \qquad K\le K_\text{max}=2mg,\)
a lánc a mozgása során nem szakad el.
Statistics:
31 students sent a solution. 5 points: Dobos Anita, Hegedüs Márk, Klement Tamás, Szabó Donát, Tóth Kolos Barnabás. 4 points: Christ Miranda Anna, Csapó András, Fajszi Karsa, Sütő Áron, Zádori Gellért. 3 points: 2 students. 2 points: 6 students. 1 point: 5 students. 0 point: 4 students.
Problems in Physics of KöMaL, April 2024
