A P. 5565. feladat (2024. április)

P. 5565. Egy hosszú, hajlékony, súlyos lánc egyik végét rögzítettük. A lelógó lánc akkor szakadna el, ha a saját súlyánál nagyobb terhet akasztanánk rá.

A láncot az ábrán látható helyzetben elengedjük. (A mozgó és a már megfeszült láncdarab is függőleges egyenesnek tekinthető.) Vajon elszakad-e a lánc?

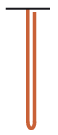
Közli: Gerencsér Jenő, Kaposvár

(5 pont)

A beküldési határidő 2024. május 15-én LEJÁRT.

I. megoldás. Legyen a lánc tömege $\displaystyle m$, a hossza $\displaystyle \ell$. Tekintsük azt a helyzetet, amelynél a lánc szabad vége $\displaystyle x$ távolságra került a rögzített láncvégtől. A lánc mozgásban lévő része ekkor $\displaystyle \frac{\ell-x}{2}$, az álló része pedig $\displaystyle \frac{\ell+x}{2}$ hosszúságú. A mozgásban lévő rész szabadon esik, benne nem ébred feszítőerő.

A szabadon eső láncdarab elmozdulása $\displaystyle t$ idő alatt

sebessége pedig

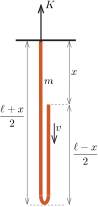
A láncot feszítő erő a jobb oldali részben nulla, a bal oldali (már megfeszült) láncdarabban pedig a felfüggesztési ponttól mért távolsággal arányosan csökken. (Ez az álló láncdarabra felírható erőegyensúly egyenletéből következik.) A feszítőerő tehát a bal oldali láncdarab felső végénél a legnagyobb. Jelöljük ezt az erőt (amelyet a mennyezet fejt ki a láncra) $\displaystyle K$-val. Amennyiben a mozgás teljes ideje alatt $\displaystyle K\le 2mg$, akkor a lánc nem fog elszakadni.

Számítsuk ki, hogy mekkora a lánc $\displaystyle I$ impulzusa $\displaystyle t$ idővel az elengedés után. Ennek a mennyiségnek időegységenkénti megváltozása, vagyis az $\displaystyle I'(t)$ derivált a láncra ható külső erők eredőjével ($\displaystyle K$ és az $\displaystyle mg$ nehézségi erő előjeles összegével) egyezik meg.

Mivel a láncdarab tömege a hosszával arányos, a mozgásban lévő rész impulzusa

$\displaystyle I(t)=\frac{m}{\ell}\cdot \frac{\ell-x(t)}{2}\cdot v(t),$

vagyis (1) és (2) behelyettesítésével

$\displaystyle I(t)=\frac{mg}{2}t-\frac{mg^2}{4\ell}t^3.$

A Newton-féle mozgásegyenlet szerint

$\displaystyle mg-K(t)=I'(t)=\frac{mg}{2}-\frac{3mg^2}{4\ell}t^2,$

vagyis

$\displaystyle K(t)=\frac{mg}{2}+\frac{3mg^2}{4\ell}t^2.$

A láncot feszítő erő a rögzített végpontjánál indulásakor $\displaystyle K(0)=\frac{mg}{2}$, az idő múltával $\displaystyle K(t)$ egyre nagyobb lesz, és a maximális értékét a lánc teljes kiegyenesedésekor, $\displaystyle T=\sqrt{\frac{2\ell}{g}}$ időpillanatban éri el.

Mivel

$\displaystyle K(T)=\frac{mg}{2}+\frac{3mg^2}{4\ell}\,\frac{2\ell}{g}=2mg$

kevesebb, mint a lánc teherbírása, a lánc biztosan nem szakad el.

II. megoldás. Kövessük az I. megoldás jelöléseit! Mialatt az $\displaystyle x$ távolság egy kicsiny $\displaystyle \Delta x$ értékkel megnő, a mozgásban lévő láncdarab tömege $\displaystyle \Delta m=\frac{\Delta x}{2\ell}m$ értékkel változik (csökken). Ekkora tömegű láncdarab sebessége $\displaystyle v=\sqrt{2gx}$-ről (rugalmatlan ütközések miatt) nullára csökken, tehát az impulzusváltozása (amit lefelé tekintünk pozitívnak)

$\displaystyle \Delta I=\Delta m\,v=\frac{mv}{2\ell}\,\Delta x$

értékkel csökken. Ezt a változást a lánc másik fele által kifejtett

$\displaystyle K^*=\frac{\Delta I}{\Delta t}$

nagyságú, felfelé irányuló erő hozza létre. ($\displaystyle \Delta t=(\Delta x)/v$ a kicsiny láncdarab lefékeződésének ideje.) Így tehát

$\displaystyle K^*=\frac{mv}{2\ell}\,\frac{\Delta x}{\Delta t}=\frac{mv^2}{2\ell}=mg\,\frac{x}{\ell}.$

Ennek az erőnek a bal oldali láncdarabra ható ellenereje ugyanekkora nagyságú, de lefelé irányuló erő.

A bal oldali láncdarabra ható erők eredője nulla:

$\displaystyle K-mg\,\frac{\ell+x}{2\ell}-K^*=0,$

vagyis

$\displaystyle K(x)=mg\,\frac{\ell+x}{2\ell}+\frac{x}{\ell}\,mg=\frac{mg}{2}\left(1+3\,\frac{x}{\ell}\right).$

Mivel

$\displaystyle x\le\ell, \qquad K\le K_\text{max}=2mg,$

a lánc a mozgása során nem szakad el.

Megjegyzés. Egy láncot kétféleképpen is modellezhetünk. Ha a felső végei kicsit távolabb vannak egymástól, és a lánc nagyon hajlékony, a láncban végig húzófeszültség lesz, és így a leeső rész gyorsulása $\displaystyle g$-nél nagyobb lehet. Ilyenkor a rendszer konzervatív. Ha a láncot közelítjük az egydimenziós esethez, elromlik a konzervativitás, a kanyarulatnál lévő láncszemek rugalmatlanul ütköznek, egy-egy láncszem impulzusa hirtelen nullává válik, és ez rántja meg a már nem mozgó részt. A feladat megoldása ezt a második értelmezést követi: az energia disszipálódik, a leeső láncdarab feszültségmentes, és így szabadon esik. (G. P.)

Statisztika:

31 dolgozat érkezett.
5 pontot kapott:	Dobos Anita, Hegedüs Márk, Klement Tamás, Szabó Donát, Tóth Kolos Barnabás.
4 pontot kapott:	Christ Miranda Anna, Csapó András, Fajszi Karsa, Sütő Áron, Zádori Gellért.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2024. áprilisi fizika feladatai