 Problem P. 5566. (April 2024)
Problem P. 5566. (April 2024)
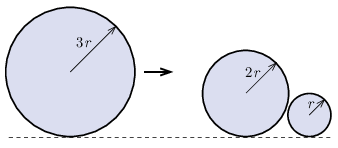
P. 5566. There are two discs of radii \(\displaystyle 2r\) and \(\displaystyle r\) at rest on a horizontal, not perfectly flat tabletop such that they almost touch each other. In the plane, a third disk of radius \(\displaystyle 3r\) slides without rotation so that its velocity vector is parallel to the common tangent of the three disks. The top view of the three disks are shown in the figure. All three disks are made of the same material and have the same height. After the collision, which is considered to be elastic, the disc with radius \(\displaystyle 3r\) slows down due to friction and stops after travelling \(\displaystyle d=5~\mathrm{cm}\). In what direction and how far will the smaller discs travel on the table? Friction between the discs is negligible. Hint: See problem P. 5555. in the March 2024 issue of this journal and the article titled Complex numbers in physics I. in this issue.
(5 pont)
Deadline expired on May 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Az ütközés nagyon rövid ideje alatt a külső erők (az asztallap és a korongok közötti súrlódás) hatása figyelmen kívül hagyható, vagyis a három korongból álló rendszer zártnak tekinthető. Az ütközések során a teljes mozgásmennyiség (impulzus) vektora állandó marad. Az ütközés rugalmas, így az ütköző korongok összes mozgási energiája sem változik meg. A korongok közötti súrlódás elhanyagolható, emiatt a korongok nem jöhetnek forgásba, vagyis a mozgási energia tisztán a transzlációs mozgásból származik.
A korongok tömege az alapterületükkel, vagyis a sugaruk négyzetével arányos: \(\displaystyle 9m\), \(\displaystyle 4m\), \(\displaystyle m\).
Vizsgáljuk először a \(\displaystyle 9m\) és a \(\displaystyle 4m\) tömegű korong ütközését. Jelöljük a nagyobb korong ütközés előtti sebességvektorát \(\displaystyle \boldsymbol{v}_0\)-lal. Az ütközés pillanatában (lásd az 1. ábrát) a korongok \(\displaystyle P\) és \(\displaystyle Q\) középpontjára illeszkedő egyenesnek a nagyobb korong kezdeti mozgásirányával bezárt szöge:
| \(\displaystyle (1)\) | \(\displaystyle \varphi=\arcsin\frac{1}{5}=11{,}54^\circ.\) |
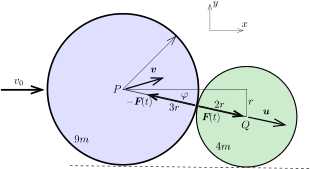
1. ábra
Az ütközés során a két korong között egy nagyon rövid ideig tartó, nagyon nagy \(\displaystyle \boldsymbol{F}(t)\) erő lép fel, ami a kezdetben álló kisebb korongot \(\displaystyle \overrightarrow{PQ}\) irányba valamekkora \(\displaystyle \boldsymbol{u}\) sebességgel meglöki. Eközben a nagyobb korong sebessége \(\displaystyle \boldsymbol{v}\)-re változik. A kisebb korong az ütközés előtt állt, így \(\displaystyle \boldsymbol{u}\) iránya nyilván megegyezik \(\displaystyle \boldsymbol{F}\) irányával.
Az ábrán látható koordináta-rendszerben az impulzusmegmaradás törvénye szerint
\(\displaystyle (9m)v_0=(9m)v_x+(4m)u\cos\varphi,\)
\(\displaystyle 0=(9m)v_y-(4m)u\sin\varphi,\)
vagyis
| \(\displaystyle (2)\) | \(\displaystyle v_x=v_0-\frac{4}{9}{u\cos\varphi},\) |
| \(\displaystyle (3)\) | \(\displaystyle v_y= \frac{4}{9}{u\sin\varphi}.\) |
Az energiamegmaradás törvényét alkalmazva felírhatjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle \frac{1}{2}(9m)v_0^2=\frac{1}{2}(9m)\left(v_x^2+v_y^2\right)+\frac{1}{2}(4m)u^2.\) |
(2)-t és (3)-t (4)-be helyettesítve az \(\displaystyle u\) sebességnagyságra egy hiányos másodfokú egyenletet kapunk, aminek az egyik (számunkra érdektelen) megoldása \(\displaystyle u=0\), a másik gyöke pedig
| \(\displaystyle (5)\) | \(\displaystyle u=\frac{18}{13}v_0\cos\varphi=\frac{18\sqrt{24}}{65}v_0\approx 1{,}36\,v_0.\) |
(2), (3) és (5) felhasználásával a korongok sebességkomponensei:
\(\displaystyle u_x=u\cos\varphi=1{,}33\,v_0,\)
\(\displaystyle u_y=-u\sin\varphi=-0{,}27\,v_0,\)
\(\displaystyle v_x=0{,}41\,v_0,\)
\(\displaystyle v_y=0{,}12\,v_0.\)
A \(\displaystyle 4m\) tömegű korong ezután ütközik az \(\displaystyle m\) tömegű álló koronggal, és a sebességük az ütközés után \(\displaystyle \boldsymbol{w}\)-re és \(\displaystyle \boldsymbol{z}\)-re változik (2. ábra). Az ütközés ferdeségére jellemző szög a második ütközésnél
\(\displaystyle \psi=\arcsin\frac{1}{3}\approx 19{,}47^\circ.\)
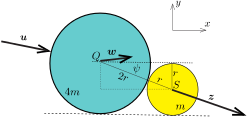
2. ábra
A legkisebb korong ütközés utáni sebessége az erőlökéssel párhuzamos, vagyis \(\displaystyle \overrightarrow{QS}\) irányú, derékszögű komponensei tehát \(\displaystyle z_x=z\cos\psi\) és \(\displaystyle z_y=-z\sin\psi\).
Erre az ütközésre is felírhatjuk a megmaradási törvényeket:
| \(\displaystyle (6)\) | \(\displaystyle (4m)u_x=(4m)w_x+m\,z_x,\) |
| \(\displaystyle (7)\) | \(\displaystyle (4m)u_y=(4m)w_y+m\,z_y,\) |
| \(\displaystyle (8)\) | \(\displaystyle \frac{1}{2}(4m)\left(u_x^2+u_y^2\right)=\frac{1}{2}(4m)\left(w_x^2+w_y^2\right)+\frac{1}{2}m\,z^2.\) |
(6) és (7)-ből kifejezve \(\displaystyle w_x\) és \(\displaystyle w_y\)-t, és ezeket (8)-ba helyettesítve \(\displaystyle z\)-re hiányos másodfokú egyenletet kapunk, aminek nullától különböző megoldása:
\(\displaystyle z=\frac{8}{5}\left(u_x\cos\psi-u_y\sin\psi\right)\approx 2{,}15\,v_0.\)
Ennek megfelelően a középső korong sebessége a második ütközés után
\(\displaystyle \boldsymbol{w}=(0{,}82;\,-0{,}09)\,v_0,\)
a legkisebb korongé
\(\displaystyle \boldsymbol{z}=(2{,}03;\,-0{,}72)\,v_0.\)
A legnagyobb korong végsebessége, mint azt korábban láttuk
\(\displaystyle \boldsymbol{v}=(0{,}41; \, 0{,}12)\,v_0.\)
Megjegyzés. Elképzelhető lenne, hogy a középső korong a második ütközés után még egyszer ütközik a legnagyobb méretű koronggal. Ez azonban a jelen esetben nem következik be, hiszen a \(\displaystyle \boldsymbol{w}-\boldsymbol{v}\) relatív sebességvektor és a korongok középpontját összekötő \(\displaystyle \overrightarrow{PQ}=(\sqrt{24};-1)\) vektor skalárszorzata pozitív, vagyis ezen két korong középpontjai a második ütközés után távolodnak egymástól.
A legnagyobb korong az eredeti mozgásirányához képes
\(\displaystyle \alpha_3=\arctg\frac{v_y}{v_x}=16{,}3^\circ\)
szögben ,,balra'' (az óramutató járásával ellentétesen) térül el, a középső korong elmozdulásának iránya
\(\displaystyle \alpha_2=\arctg\frac{\vert w_y\vert}{w_x}=6{,}3^\circ,\)
míg a legkisebb korong
\(\displaystyle \alpha_2=\arctg\frac{\vert z_y\vert}{z_x}=-19{,}5^\circ\)
szögben ,,jobbra'' (az óramutató járásával megegyező irányba) térül el.
Az asztallapon csúszó korongok az asztallal való súrlódásuk miatt ugyanolyan ütemben (\(\displaystyle a=-\mu g\) ,,gyorsulással'') egyenletesen lassulva mozognak, a megállásukig megtett útjuk a kezdősebességük négyzetével arányos. Mivel
\(\displaystyle v^2:w^2:z^2=0{,}18:0{,}68:4{,}62\approx 5\,\mathrm{cm}:19\,\mathrm{cm}:128\,\mathrm{cm},\)
ha a legnagyobb korong \(\displaystyle d=5\,\mathrm{cm}\) út megtétele után áll meg, akkor a középső kb. \(\displaystyle 19\,\mathrm{cm}\)-re jut el, a legkisebb pedig majdnem \(\displaystyle 1{,}3\,\mathrm{m}\) utat tesz meg a megállásáig.
II. megoldás. A feladat a hivatkozott cikk összefüggései segítségével is megoldható. Az I. megoldás jelöléseit követjük, és a síkbeli vektoroknak komplex számokat feleltetünk meg. Így pl. \(\displaystyle \boldsymbol{v}=(v_x,v_y)\) komplex megfelelője a \(\displaystyle v=v_x+iv_y,\) és hasonlóan a többi vektornál is. (Figyelem: Az I. megoldásban \(\displaystyle v\) a \(\displaystyle \boldsymbol{v}\) vektor nagyságát jelölte, itt viszont a teljes \(\displaystyle \boldsymbol{v}\) vektornak megfeleltetett komplex számmal egyezik meg.)
Ha egy nagyobb korong \(\displaystyle \boldsymbol{v}_0\) sebességgel nekiütközik a nála \(\displaystyle k\)-szor kisebb tömegű álló korongnak, akkor az idézett cikk képleteinek megfelelően az ütközés után a nagyobb korong sebessége
\(\displaystyle v=\frac{kv_0+\mathrm{e}^{2i\alpha}\,\overline{v_0}}{k+1},\)
a kisebb korongé pedig
\(\displaystyle u=\frac{k}{k+1}(v_0-\mathrm{e}^{2i\alpha}\,\overline{v_0}).\)
A fenti képletekben \(\displaystyle \alpha\) a korongok közös érintőjének a Gauss-számsík valós tengelyével bezárt szöge.
Az első ütközésnél \(\displaystyle k=\frac{9}{4}=2{,}25\), valamint
\(\displaystyle \alpha=\frac{\pi}{2}-\varphi=\arccos\frac{1}{5}=78{,}46^\circ=1{,}369\,\mathrm{rad},\)
és ennek megfelelően
\(\displaystyle \mathrm{e}^{2i\alpha}=-0{,}921+0{,}392\,i.\)
(A továbbiakban ezt a komplex számot \(\displaystyle q\)-val fogjuk jelölni.)
Válasszuk a legnagyobb korong ütközés előtti sebességének \(\displaystyle \vert\boldsymbol{v}_0\vert\) nagyságát 1-nek. Ekkor a legnagyobb korong kezdeti sebessége \(\displaystyle v_0=1+0\cdot i=1\) valós szám, aminek a komplex konjugáltja is ugyanekkora.
Az ütközés utáni sebességek
\(\displaystyle v=\frac{2{,}25+q}{3{,}25}=0{,}409+0{,}121\,i,\qquad\textrm{valamint}\qquad u=\frac{2{,}25}{3{,}25}(1-q)=1{,}329-0{,}271\,i.\)
Megjegyzés. A komplex számok közötti algebrai műveleteket akár ,,kézzel'', egy zsebszámológéppel is elvégezhetjük, de a GeoGebra vagy a WolframAlpha program segítségével sokkal gyorsabban és kényelmesebben célhoz érhetünk.
A második ütközésnél a tömegarány \(\displaystyle k'=4\), valamint
\(\displaystyle \alpha'=\frac{\pi}{2}-\psi=\arccos\frac{1}{3},\)
és ennek megfelelően
\(\displaystyle q'=\mathrm{e}^{2i\alpha'}=-0{,}778+0{,}629\,i.\)
A középső (\(\displaystyle 2r\) sugarú) korong ütközés előtti sebességét az első ütközésnél kiszámított \(\displaystyle u\) komplex számmal adhatjuk meg.
A második ütközés utáni sebességek:
\(\displaystyle w=\frac{4u+q'\overline{u}}{5}=0{,}823-0{,}092\,i,\qquad\textrm{illetve}\qquad z=\frac{4}{5}(u-q\overline{u} )=2{,}027-0{,}717\,i.\)
A korongok ütközések utáni sebességnégyzeteinek aránya
\(\displaystyle v\overline{v}:w\overline{w}:z\overline{z}=0{,}18:0{,}68:4{,}62,\)
és ugyanilyen arányban állnak a megállásukig megtett utak is.
Statistics:
19 students sent a solution. 5 points: Czirják Márton Pál, Dobos Anita, Fehérvári Donát, Szabó Donát. 4 points: Bélteki Teó, Hornok Máté, Kiss 131 Adorján Timon. 3 points: 1 student. 2 points: 5 students. 1 point: 1 student. 0 point: 1 student.
Problems in Physics of KöMaL, April 2024
