A P. 5567. feladat (2024. április)

P. 5567. Vákuumba helyezett, peremes kialakítású, $\displaystyle h$ magasságú, hőszigetelő tartály vízszintes asztalon áll. A tartályban kezdetben $\displaystyle p_0$ nyomású gáz található, melyet felülről egy hőszigetelő, könnyű dugattyú zár le, a tartály magasságának felénél pedig hővezető, vékony, könnyű dugattyú található. A tartály felső felében egyatomos, alul kétatomos gáz található. A felső dugattyúra óvatosan egy nagyon nehéz terhet helyezünk, majd elengedjük azt. A dugattyúk mozgása – a gázok belső súrlódása miatt – jónéhány lengés után megáll. Hol helyezkednek el a dugattyúk az egyensúlyi helyzetükben?

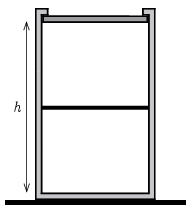
Közli: Berke Martin, Budapest

(5 pont)

A beküldési határidő 2024. május 15-én LEJÁRT.

Megoldás. A tartály fala és a felső dugattyú hőszigetelő, a tartály körül vákuum van, így a tartályban lévő gázokból és a ráhelyezett ,,nagyon nehéz'' testből álló rendszer összenergiája állandó.

Az elválasztó dugattyú könnyű és hővezető, így egyensúlyban a két térrészben a gázok nyomása és hőmérséklete is megegyezik. Kezdetben a két térrész térfogata egyforma (tehát az azonos nyomás és hőmérséklet miatt a két térrészben a gázok anyagmennyisége is ugyanakkora), így a végső egyensúlyban is azonos lesz a térfogatuk. Jelöljük az alsó dugattyú keresett magasságát $\displaystyle x$-szel, akkor a felső dugattyú magassága $\displaystyle 2x$ lesz.

Írjuk fel az energiamegmaradást a kezdeti és végső egyensúlyi állapotokra:

ahol $\displaystyle A$ a henger keresztmetszete, $\displaystyle M$ a ráhelyezett test tömeg, $\displaystyle g$ a nehézségi gyorsulás, $\displaystyle p$ pedig a gázok nyomása a végső egyensúlyi állapotban. Egyensúlyban a test súlyát a dugattyúnak kell megtartania, ezért

(2)-t (1)-be beírva és rendezve:

$\displaystyle x=\frac{p+2p_0}{6p}h.$

A feladat szövege szerint a ráhelyezett test ,,nagyon nehéz'', így

$\displaystyle p=\frac{Mg}{A}\gg p_0,$

azaz

$\displaystyle p+2p_0\approx p\qquad\textrm{és}\qquad x=\frac{h}{6}.$

A dugattyúk tehát az egyensúlyi helyzetükben a tartály aljától $\displaystyle h/6$ és $\displaystyle h/3$ magasságban lesznek.

Statisztika:

19 dolgozat érkezett.
5 pontot kapott:	Bencz Benedek, Debreceni Dániel, Szabó Donát, Tóth Kolos Barnabás.
4 pontot kapott:	Csapó András, Csiszár András, Erős Fanni, Fajszi Karsa, Fehérvári Donát, Sütő Áron.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2024. áprilisi fizika feladatai