 Problem P. 5570. (April 2024)
Problem P. 5570. (April 2024)
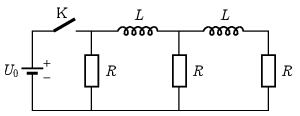
P. 5570. The circuit – containing three identical resistors and two identical coils – shown in the figure has been connected to a DC source for a relatively long time. (The resistance of the coils is negligible.)
\(\displaystyle a)\) What will be the current flowing through the resistors immediately after switch K is turned off?
\(\displaystyle b)\) What is the value of the induced electromotive force in each coil, right after switch K is turned off?
\(\displaystyle c)\) How do the sum and difference of the currents in the coils vary in time?
\(\displaystyle d)\) How long does it take for the current in one coil and the current in the other coil to drop to half of the current measured very soon after switch K was turned off?
Data: \(\displaystyle U_0=1~\mathrm{V}\), \(\displaystyle L=1~\mathrm{H}\), \(\displaystyle R=1\,\Omega\).
(6 pont)
Deadline expired on May 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) A kapcsoló kikapcsolása előtt a ,,viszonylag hosszú'' idő miatt időben állandó áramok folynak, így a tekercsek olyanok, mintha (elhanyagolható ohmos ellenállású) vezetékek lennének. Eszerint a kapcsoló kikapcsolása előtt mindhárom ellenálláson
\(\displaystyle I_0=\frac{U_0}{R}=1\,\mathrm{A}\)
nagyságú áram folyik. Jelöljük a telephez közelebbi tekercset 1-es, a távolabbit 2-es indexszel. A tekercseken a csomóponti törvény szerint a kapcsoló kikapcsolása előtt \(\displaystyle I_1(t<0)=2I_0\), illetve \(\displaystyle I_2(t<0)=I_0\) áram folyt (1. ábra).
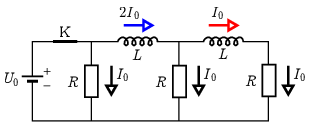
1. ábra
A tekercsek árama nem változhat ugrásszerűen, ezért a kapcsoló kikapcsolása után közvetlenül ugyanekkora marad:
\(\displaystyle I_1(0)=2I_0,\qquad I_2(0)=I_0.\)
A három ellenálláson – ismét a csomóponti törvény alapján – ekkor rendre
\(\displaystyle I_{R1}=-2I_0=-2\,\mathrm{A},\quad I_{R2}=I_0=1\,\mathrm{A}\quad\textrm{és}\quad I_{R3}=I_0=1\,\mathrm{A}\)
áramok folynak. (Az áram irányát az ellenállásokon lefelé vesszük pozitívnak – lásd a 2. ábrát.)
Az ellenállásokon természetesen változhat az áramerősség ugrásszerűen is: az első ellenálláson a kapcsoló kinyitásakor hirtelen \(\displaystyle -2\)-szeresére változik.
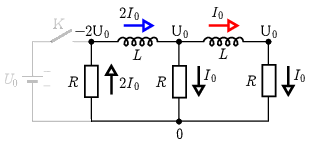
2. ábra
\(\displaystyle b)\) Az ellenállásokon \(\displaystyle U_R=RI_R\) feszültség esik, így a tekercsek végpontjainak feszültsége az ellenállások közös csomópontjához viszonyítva \(\displaystyle -2U_0\), \(\displaystyle U_0\) és \(\displaystyle U_0\) (2. ábra). Ez alapján a tekercseken indukálódott feszültség közvetlenül a kapcsoló kikapcsolása után:
\(\displaystyle U_1(0)=-3U_0=-3\,\mathrm{V},\qquad U_2(0)=0.\)
\(\displaystyle c)\) Ezután vizsgáljuk az áramok változását a kapcsoló kikapcsolása után. Ha egy \(\displaystyle L\) induktivitású tekercs árama időben változik, akkor a tekercsen
\(\displaystyle U_L=L\frac{\mathrm{d}I}{\mathrm{d}t}\)
feszültség esik.
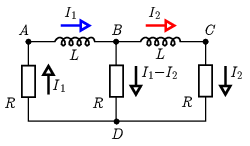
3. ábra
Írjuk fel a huroktörvényt először az \(\displaystyle ABCDA\) hurokra (3. ábra):
\(\displaystyle L\frac{\mathrm{d}I_1}{\mathrm{d}t}+L\frac{\mathrm{d}I_2}{\mathrm{d}t}+RI_2+RI_1=0,\)
amit rendezve:
\(\displaystyle \frac{\mathrm{d}(I_1+I_2)}{\mathrm{d}t}=\frac{\mathrm{d}I_1}{\mathrm{d}t}+\frac{\mathrm{d}I_2}{\mathrm{d}t}=-\frac{R}{L}(I_1+I_2)\)
egyenletet kapjuk. Ez az egyenlet ugyanolyan (az \(\displaystyle I_1+I_2\) mennyiségre), mint a jól ismert radioaktív bomlástörvény (a magok \(\displaystyle N\) számára):
\(\displaystyle \frac{\mathrm{d}(N)}{\mathrm{d}t}=-\lambda N,\)
amelynek a megoldását is ismerjük:
\(\displaystyle N(t)=N_0\,\mathrm{e}^{-\lambda t}.\)
Az analógia alapján a megoldás:
\(\displaystyle I_1(t)+I_2(t)=3I_0\,\mathrm{e}^{-t/\tau_1},\)
ahol
\(\displaystyle \tau_1=\frac{L}{R}=1\,\mathrm{s}\)
az exponenciális lecsengés időállandója.
Másodszor írjuk fel a huroktörvényt a (nyolcas alakú) \(\displaystyle ABDCBDA\) hurokra:
\(\displaystyle L\frac{\mathrm{d}I_1}{\mathrm{d}t}+R(I_1-I_2)-RI_2-L\frac{\mathrm{d}I_2}{\mathrm{d}t}+R(I_1-I_2)+RI_1=0,\)
amit rendezve most a
\(\displaystyle \frac{\mathrm{d}(I_1-I_2)}{\mathrm{d}t}=\frac{\mathrm{d}I_1}{\mathrm{d}t}-\frac{\mathrm{d}I_2}{\mathrm{d}t}=-\frac{3R}{L}(I_1-I_2)\)
egyenletet kapjuk. Ennek megoldása az előzőhöz hasonlóan:
\(\displaystyle I_1(t)-I_2(t)=I_0\,\mathrm{e}^{-t/\tau_2},\)
ahol
\(\displaystyle \tau_2=\frac{L}{3R}=\frac{1}{3}\,\mathrm{s}\)
az időállandó.
A tekercseken folyó áramerősségek összege, illetve különbsége tehát:
$$\begin{align*} I_{+}(t)=I_1(t)+I_2(t)&=3I_0\,\mathrm{e}^{-t/\tau_1}=3\,\mathrm{A}\cdot\mathrm{e}^{-t/1\,\mathrm{s}},\\ I_{-}(t)=I_1(t)-I_2(t)&=I_0\,\mathrm{e}^{-t/\tau_2}=1\,\mathrm{A}\cdot\mathrm{e}^{-3t/1\,\mathrm{s}}. \end{align*}$$\(\displaystyle d)\) Azt keressük, hogy az egyes tekercseken mekkora \(\displaystyle t_1\), illetve \(\displaystyle t_2\) idő alatt csökken az áramerősség a kapcsoló nyitása után közvetlen mért érték felére. \(\displaystyle I_1(t_1)\)-t és \(\displaystyle I_2(t_2)\)-t írjuk fel az előző rész megoldása alapján, majd tegyük egyenlővé a kezdeti értékek felével:
$$\begin{align*} I_1(t_1)&=\frac{I_{+}(t_1)+I_{-}(t_1)}{2}=\frac{3I_0}{2}\,\mathrm{e}^{-t_1/\tau_1}+\frac{I_0}{2}\,\mathrm{e}^{-t_1/\tau_2}=\frac{I_1(0)}{2}=I_0,\\ I_2(t_2)&=\frac{I_{+}(t_2)-I_{-}(t_2)}{2}=\frac{3I_0}{2}\,\mathrm{e}^{-t_"/\tau_1}-\frac{I_0}{2}\,\mathrm{e}^{-t_"/\tau_2}=\frac{I_2(0)}{2}=\frac{I_0}{2}. \end{align*}$$Ezekből a keresett időkre a
$$\begin{align*} 3\,\mathrm{e}^{-t_1/\tau_1}+\mathrm{e}^{-t_1/\tau_2}&=2,\\ 3\,\mathrm{e}^{-t_2/\tau_1}-\mathrm{e}^{-t_2/\tau_2}&=1 \end{align*}$$egyenleteket kapjuk.
Vezessük be az
\(\displaystyle a_1=\mathrm{e}^{-t_1/\tau_1},\quad\textrm{illetve}\quad a_2=\mathrm{e}^{-t_2/\tau_1}\)
jelöléseket. Ekkor, felhasználva, hogy \(\displaystyle \tau_2=\tfrac{1}{3}\tau_1\):
\(\displaystyle \mathrm{e}^{-t_1/\tau_2}=\mathrm{e}^{-3t_1/\tau_1}=a_1^3\quad\textrm{és}\quad\mathrm{e}^{-t_2/\tau_2}=\mathrm{e}^{-3t_2/\tau_1}=a_2^3,\)
és az egyenletek az
$$\begin{align*} a_1^3+3a_1-2&=0,\\ a_2^3-3a_2+1&=0 \end{align*}$$alakra egyszerűsödnek. Ezeket a harmadfokú egyenleteket meg lehet oldani internetes program segítségével, numerikus próbálgatással, grafikusan vagy a Cardano-képlettel. Az első egyenletnek csak egy valós gyöke van:
\(\displaystyle a_1\approx 0{,}596,\)
amiből
\(\displaystyle t_1=-\tau_1\ln a_1\approx 0{,}517\,\mathrm{s}.\)
A második egyenletnek három valós megoldása van, közelítőleg: \(\displaystyle -1{,}879\), \(\displaystyle 0{,}347\) és \(\displaystyle 1{,}532\). Az első, negatív gyök nyilván nem lehet jó, hiszen szükségszerűen \(\displaystyle a_2>0\), a harmadik gyök pedig negatív \(\displaystyle t_2\) értéket eredményezne. Így az egyetlen fizikailag értelmezhető megoldás:
\(\displaystyle a_2\approx 0{,}347,\)
amiből
\(\displaystyle t_2=-\tau_1\ln a_2\approx 1{,}058\,\mathrm{s}.\)
A tekercsek áramerőssége tehát \(\displaystyle t_1\approx 0{,}517\,\mathrm{s}\), illetve \(\displaystyle t_2\approx 1{,}058\,\mathrm{s}\) idő alatt csökken a kezdeti áramerősségek felére.
Megjegyzés. Nem része a feladatnak, de a felírt függvények alapján ábrázolhatjuk az időfüggvényeket. A 4. ábrán a két tekercs áramának összege és különbsége látható – ezek egyszerű exponenciális függvények.
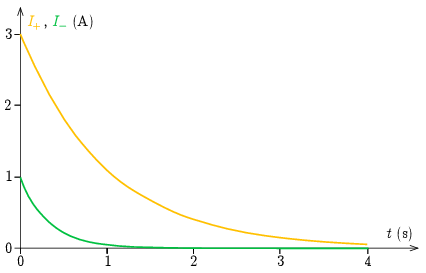
4. ábra
Az 5. ábrán \(\displaystyle I_1(t)\) és \(\displaystyle I_2(t)\) látható, a grafikonról leolvashatók a keresett ,,felezési idők'' is.
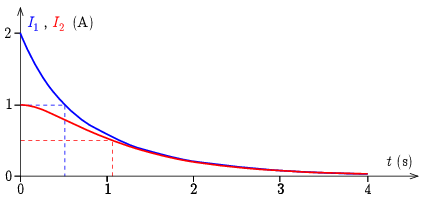
5. ábra
A 6. ábrán a tekercsek \(\displaystyle U_1(t)\) és \(\displaystyle U_2(t)\) feszültségét ábrázoltuk. A feszültségek arányosak az áramok változási sebességeivel. Jól megfigyelhető, hogy \(\displaystyle I_2\)-nek \(\displaystyle t=0\) nál vízszintes az érintője, összhangban azzal, hogy \(\displaystyle U_2(0)=0\).
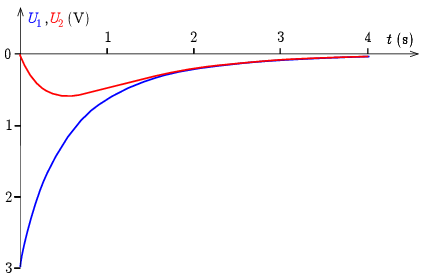
6. ábra
Statistics:
11 students sent a solution. 6 points: Bencz Benedek, Fajszi Karsa, Hegedüs Márk, Kiss 131 Adorján Timon, Klement Tamás, Seprődi Barnabás Bendegúz, Tóth Kolos Barnabás. 4 points: 2 students. 3 points: 1 student.
Problems in Physics of KöMaL, April 2024
