 |
A P. 5570. feladat (2024. április) |
P. 5570. Az ábrán látható – három egyforma ellenállást és két egyforma tekercset tartalmazó – hálózatot viszonylag hosszú ideje egyenáramú forrásra kapcsoltuk. (A tekercsek ohmikus ellenállása elhanyagolható.)
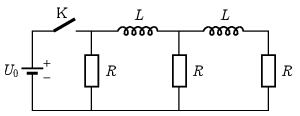
\(\displaystyle a)\) Mekkora áram fog folyni az ellenállásokon közvetlenül a K kapcsoló kikapcsolása után?
\(\displaystyle b)\) Mekkora feszültség indukálódik a tekercsekben közvetlenül a K kapcsoló kikapcsolása után?
\(\displaystyle c)\) Hogyan változik időben a tekercseken folyó áramerősségek összege, illetve különbsége?
\(\displaystyle d)\) Mennyi idő múlva csökken az egyik, illetve a másik tekercs áramerőssége a K kapcsoló kikapcsolása után nagyon hamar mérhető áramerősség felére?
Adatok: \(\displaystyle U_0=1~\mathrm{V}\), \(\displaystyle L=1~\mathrm{H}\), \(\displaystyle R=1~\Omega\).
Károlyházy Frigyes (1929-2012) feladata nyomán
(6 pont)
A beküldési határidő 2024. május 15-én LEJÁRT.
Megoldás. \(\displaystyle a)\) A kapcsoló kikapcsolása előtt a ,,viszonylag hosszú'' idő miatt időben állandó áramok folynak, így a tekercsek olyanok, mintha (elhanyagolható ohmos ellenállású) vezetékek lennének. Eszerint a kapcsoló kikapcsolása előtt mindhárom ellenálláson
\(\displaystyle I_0=\frac{U_0}{R}=1\,\mathrm{A}\)
nagyságú áram folyik. Jelöljük a telephez közelebbi tekercset 1-es, a távolabbit 2-es indexszel. A tekercseken a csomóponti törvény szerint a kapcsoló kikapcsolása előtt \(\displaystyle I_1(t<0)=2I_0\), illetve \(\displaystyle I_2(t<0)=I_0\) áram folyt (1. ábra).
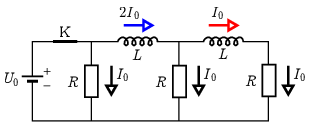
1. ábra
A tekercsek árama nem változhat ugrásszerűen, ezért a kapcsoló kikapcsolása után közvetlenül ugyanekkora marad:
\(\displaystyle I_1(0)=2I_0,\qquad I_2(0)=I_0.\)
A három ellenálláson – ismét a csomóponti törvény alapján – ekkor rendre
\(\displaystyle I_{R1}=-2I_0=-2\,\mathrm{A},\quad I_{R2}=I_0=1\,\mathrm{A}\quad\textrm{és}\quad I_{R3}=I_0=1\,\mathrm{A}\)
áramok folynak. (Az áram irányát az ellenállásokon lefelé vesszük pozitívnak – lásd a 2. ábrát.)
Az ellenállásokon természetesen változhat az áramerősség ugrásszerűen is: az első ellenálláson a kapcsoló kinyitásakor hirtelen \(\displaystyle -2\)-szeresére változik.
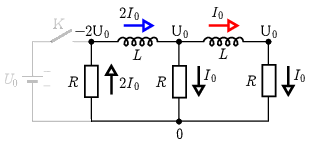
2. ábra
\(\displaystyle b)\) Az ellenállásokon \(\displaystyle U_R=RI_R\) feszültség esik, így a tekercsek végpontjainak feszültsége az ellenállások közös csomópontjához viszonyítva \(\displaystyle -2U_0\), \(\displaystyle U_0\) és \(\displaystyle U_0\) (2. ábra). Ez alapján a tekercseken indukálódott feszültség közvetlenül a kapcsoló kikapcsolása után:
\(\displaystyle U_1(0)=-3U_0=-3\,\mathrm{V},\qquad U_2(0)=0.\)
\(\displaystyle c)\) Ezután vizsgáljuk az áramok változását a kapcsoló kikapcsolása után. Ha egy \(\displaystyle L\) induktivitású tekercs árama időben változik, akkor a tekercsen
\(\displaystyle U_L=L\frac{\mathrm{d}I}{\mathrm{d}t}\)
feszültség esik.
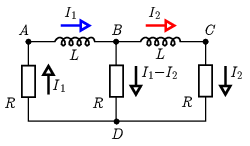
3. ábra
Írjuk fel a huroktörvényt először az \(\displaystyle ABCDA\) hurokra (3. ábra):
\(\displaystyle L\frac{\mathrm{d}I_1}{\mathrm{d}t}+L\frac{\mathrm{d}I_2}{\mathrm{d}t}+RI_2+RI_1=0,\)
amit rendezve:
\(\displaystyle \frac{\mathrm{d}(I_1+I_2)}{\mathrm{d}t}=\frac{\mathrm{d}I_1}{\mathrm{d}t}+\frac{\mathrm{d}I_2}{\mathrm{d}t}=-\frac{R}{L}(I_1+I_2)\)
egyenletet kapjuk. Ez az egyenlet ugyanolyan (az \(\displaystyle I_1+I_2\) mennyiségre), mint a jól ismert radioaktív bomlástörvény (a magok \(\displaystyle N\) számára):
\(\displaystyle \frac{\mathrm{d}(N)}{\mathrm{d}t}=-\lambda N,\)
amelynek a megoldását is ismerjük:
\(\displaystyle N(t)=N_0\,\mathrm{e}^{-\lambda t}.\)
Az analógia alapján a megoldás:
\(\displaystyle I_1(t)+I_2(t)=3I_0\,\mathrm{e}^{-t/\tau_1},\)
ahol
\(\displaystyle \tau_1=\frac{L}{R}=1\,\mathrm{s}\)
az exponenciális lecsengés időállandója.
Másodszor írjuk fel a huroktörvényt a (nyolcas alakú) \(\displaystyle ABDCBDA\) hurokra:
\(\displaystyle L\frac{\mathrm{d}I_1}{\mathrm{d}t}+R(I_1-I_2)-RI_2-L\frac{\mathrm{d}I_2}{\mathrm{d}t}+R(I_1-I_2)+RI_1=0,\)
amit rendezve most a
\(\displaystyle \frac{\mathrm{d}(I_1-I_2)}{\mathrm{d}t}=\frac{\mathrm{d}I_1}{\mathrm{d}t}-\frac{\mathrm{d}I_2}{\mathrm{d}t}=-\frac{3R}{L}(I_1-I_2)\)
egyenletet kapjuk. Ennek megoldása az előzőhöz hasonlóan:
\(\displaystyle I_1(t)-I_2(t)=I_0\,\mathrm{e}^{-t/\tau_2},\)
ahol
\(\displaystyle \tau_2=\frac{L}{3R}=\frac{1}{3}\,\mathrm{s}\)
az időállandó.
A tekercseken folyó áramerősségek összege, illetve különbsége tehát:
$$\begin{align*} I_{+}(t)=I_1(t)+I_2(t)&=3I_0\,\mathrm{e}^{-t/\tau_1}=3\,\mathrm{A}\cdot\mathrm{e}^{-t/1\,\mathrm{s}},\\ I_{-}(t)=I_1(t)-I_2(t)&=I_0\,\mathrm{e}^{-t/\tau_2}=1\,\mathrm{A}\cdot\mathrm{e}^{-3t/1\,\mathrm{s}}. \end{align*}$$\(\displaystyle d)\) Azt keressük, hogy az egyes tekercseken mekkora \(\displaystyle t_1\), illetve \(\displaystyle t_2\) idő alatt csökken az áramerősség a kapcsoló nyitása után közvetlen mért érték felére. \(\displaystyle I_1(t_1)\)-t és \(\displaystyle I_2(t_2)\)-t írjuk fel az előző rész megoldása alapján, majd tegyük egyenlővé a kezdeti értékek felével:
$$\begin{align*} I_1(t_1)&=\frac{I_{+}(t_1)+I_{-}(t_1)}{2}=\frac{3I_0}{2}\,\mathrm{e}^{-t_1/\tau_1}+\frac{I_0}{2}\,\mathrm{e}^{-t_1/\tau_2}=\frac{I_1(0)}{2}=I_0,\\ I_2(t_2)&=\frac{I_{+}(t_2)-I_{-}(t_2)}{2}=\frac{3I_0}{2}\,\mathrm{e}^{-t_"/\tau_1}-\frac{I_0}{2}\,\mathrm{e}^{-t_"/\tau_2}=\frac{I_2(0)}{2}=\frac{I_0}{2}. \end{align*}$$Ezekből a keresett időkre a
$$\begin{align*} 3\,\mathrm{e}^{-t_1/\tau_1}+\mathrm{e}^{-t_1/\tau_2}&=2,\\ 3\,\mathrm{e}^{-t_2/\tau_1}-\mathrm{e}^{-t_2/\tau_2}&=1 \end{align*}$$egyenleteket kapjuk.
Vezessük be az
\(\displaystyle a_1=\mathrm{e}^{-t_1/\tau_1},\quad\textrm{illetve}\quad a_2=\mathrm{e}^{-t_2/\tau_1}\)
jelöléseket. Ekkor, felhasználva, hogy \(\displaystyle \tau_2=\tfrac{1}{3}\tau_1\):
\(\displaystyle \mathrm{e}^{-t_1/\tau_2}=\mathrm{e}^{-3t_1/\tau_1}=a_1^3\quad\textrm{és}\quad\mathrm{e}^{-t_2/\tau_2}=\mathrm{e}^{-3t_2/\tau_1}=a_2^3,\)
és az egyenletek az
$$\begin{align*} a_1^3+3a_1-2&=0,\\ a_2^3-3a_2+1&=0 \end{align*}$$alakra egyszerűsödnek. Ezeket a harmadfokú egyenleteket meg lehet oldani internetes program segítségével, numerikus próbálgatással, grafikusan vagy a Cardano-képlettel. Az első egyenletnek csak egy valós gyöke van:
\(\displaystyle a_1\approx 0{,}596,\)
amiből
\(\displaystyle t_1=-\tau_1\ln a_1\approx 0{,}517\,\mathrm{s}.\)
A második egyenletnek három valós megoldása van, közelítőleg: \(\displaystyle -1{,}879\), \(\displaystyle 0{,}347\) és \(\displaystyle 1{,}532\). Az első, negatív gyök nyilván nem lehet jó, hiszen szükségszerűen \(\displaystyle a_2>0\), a harmadik gyök pedig negatív \(\displaystyle t_2\) értéket eredményezne. Így az egyetlen fizikailag értelmezhető megoldás:
\(\displaystyle a_2\approx 0{,}347,\)
amiből
\(\displaystyle t_2=-\tau_1\ln a_2\approx 1{,}058\,\mathrm{s}.\)
A tekercsek áramerőssége tehát \(\displaystyle t_1\approx 0{,}517\,\mathrm{s}\), illetve \(\displaystyle t_2\approx 1{,}058\,\mathrm{s}\) idő alatt csökken a kezdeti áramerősségek felére.
Megjegyzés. Nem része a feladatnak, de a felírt függvények alapján ábrázolhatjuk az időfüggvényeket. A 4. ábrán a két tekercs áramának összege és különbsége látható – ezek egyszerű exponenciális függvények.
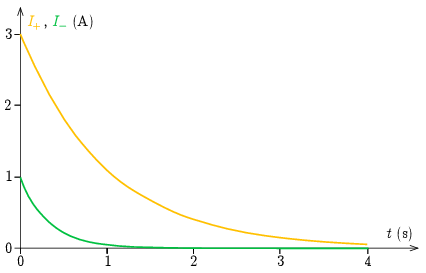
4. ábra
Az 5. ábrán \(\displaystyle I_1(t)\) és \(\displaystyle I_2(t)\) látható, a grafikonról leolvashatók a keresett ,,felezési idők'' is.
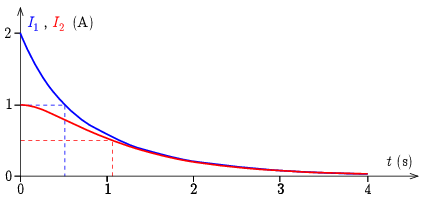
5. ábra
A 6. ábrán a tekercsek \(\displaystyle U_1(t)\) és \(\displaystyle U_2(t)\) feszültségét ábrázoltuk. A feszültségek arányosak az áramok változási sebességeivel. Jól megfigyelhető, hogy \(\displaystyle I_2\)-nek \(\displaystyle t=0\) nál vízszintes az érintője, összhangban azzal, hogy \(\displaystyle U_2(0)=0\).
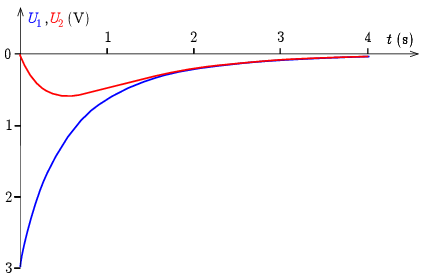
6. ábra
Statisztika:
11 dolgozat érkezett. 6 pontot kapott: Bencz Benedek, Fajszi Karsa, Hegedüs Márk, Kiss 131 Adorján Timon, Klement Tamás, Seprődi Barnabás Bendegúz, Tóth Kolos Barnabás. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 1 versenyző.
A KöMaL 2024. áprilisi fizika feladatai