A P. 5571. feladat (2024. május)

P. 5571. Egy $\displaystyle h$ magasságú asztal sarka felett ugyancsak $\displaystyle h$ magasságból egy kicsiny golyót ejtünk el. Az asztal sarkától legfeljebb milyen távol érkezhet a golyó a talajra? Az ütközést tekintsük tökéletesen rugalmasnak.

Közli: Simon Péter, Pécs

(5 pont)

A beküldési határidő 2024. június 17-én LEJÁRT.

I. megoldás. A mozgás első szakaszában a golyó szabadeséssel megtesz $\displaystyle h$ utat, majd $\displaystyle v=\sqrt{2gh}$ sebességgel az asztal sarkához érkezik. Innen ugyanakkora sebességgel ismeretlen szögben elpattan (ferde hajítás), és szintén $\displaystyle h$ távolsággal mélyebben talajt ér. A ferde hajítások következő tulajdonságát fogjuk kihasználni: a $\displaystyle v$ sebességgel elhajított test $\displaystyle t$ idő múlva $\displaystyle vt$ távolságra lesz az ugyanakkor, ugyanonnan álló helyzetből induló, szabadeséssel gyorsuló képzeletbeli ponttól. Ez a pont $\displaystyle t$ időpontban a talajtól $\displaystyle h-\tfrac{1}{2}gt^2$ magasságban lesz. A két távolságból Pitagorasz tétellel kapjuk meg a hajítás $\displaystyle d$ vízszintes távolságát a $\displaystyle t$ ideig repülő golyóra:

$\displaystyle d^2=(vt)^2-\left(h-\frac{1}{2}gt^2\right)^2=-\frac{1}{4}g^2t^4+3hgt^2-h^2,$

ahol a második lépésben behelyettesítettük $\displaystyle v$ ismert értékét. A jobb oldali kifejezés az időnek negyedfokú, $\displaystyle t^2$-nek másodfokú polinomja, és csak egy bizonyos időtartományban pozitív – amikor talajt érhet a golyó. Hogy megtaláljuk az idő szerinti maximumát, alakítsuk teljes négyzetté:

$\displaystyle d^2=-\left(\frac{1}{2}gt^2-3h\right)^2+8h^2.$

Ezen már látszik, hogy akkor van maximuma, amikor a zárójelen belüli kifejezés zérus, azaz amikor $\displaystyle t=\sqrt{\tfrac{6h}{g}}$ ideig tart a ferde hajítás. A maximum értéke $\displaystyle d_\mathrm{max}^2=8h^2$, vagyis a vízszintes távolság maximuma

$\displaystyle d_\mathrm{max}=2\sqrt2h.$

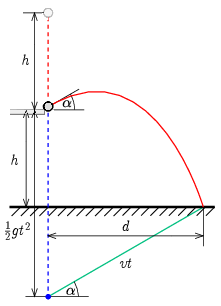
II. megoldás. A golyó az asztal sarkától a vízszintessel $\displaystyle \alpha$ szöget bezáró, $\displaystyle v=\sqrt{2gh}$ nagyságú sebességgel pattan el. A pályához tartozó vízszintes és függőleges elmozdulás:

ahol $\displaystyle t$ a repülési idő. A fenti két egyenletből álló egyenletrendszerben $\displaystyle t$-t és $\displaystyle \alpha$-t tekintjük ismeretlennek, és a maximális $\displaystyle d$-t keressük, ami mellett létezik rájuk megoldás. A két ismeretlen közül $\displaystyle \alpha$-t ejtsük ki először a következőképpen: fejezzük ki az első egyenletből $\displaystyle \cos\alpha$-t, a másodikból $\displaystyle \sin\alpha$-t:

Ezután a $\displaystyle \sin^2\alpha+\cos^2\alpha=1$ azonosságot alkalmazva kiküszöböljük az $\displaystyle \alpha$ ismeretlent:

$\displaystyle \left(\frac{\frac{1}{2}gt^2-h}{\sqrt{2gh}t}\right)^2+\left(\frac{d}{\sqrt{2gh}t}\right)^2=1,$

amit kicsit átrendezve az I. megoldás induló egyenletéhez jutunk.

Statisztika:

38 dolgozat érkezett.
5 pontot kapott:	Csiszár András, Csóka Péter, Czirják Márton Pál, Debreceni Dániel, Dobos Anita, Fehérvári Donát, Fekete Lúcia, Gerendás Roland, Hegedüs Márk, Kiss 131 Adorján Timon, Seprődi Barnabás Bendegúz, Simon János Dániel, Szabó Donát, Tóth Hanga Katalin, Tóth Kolos Barnabás, Zólomy Csanád Zsolt.
4 pontot kapott:	Bélteki Teó, Bencze Mátyás, Klement Tamás, Masa Barnabás, Tárnok Ede .
2 pontot kapott:	3 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	5 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2024. májusi fizika feladatai