Problem P. 5572. (May 2024)

P. 5572. Alistair, whose mass is 60 kg, attempts a bungee jump from a 50 m high bridge (measured from the water level). The length of the rope is adjusted so that Alistair just touches the surface of the water during the jump. Thus, his very light but sufficiently flexible rope has a spring constant of 72 N/m. Benedict, whose mass 80 kg, will attempt a similar jump. His rope is of the same quality as Alistair's, but shorter.

\(\displaystyle a)\) How long are Alistair's and Benedict's bungee ropes? What is the spring constant of Benedict's rope?

\(\displaystyle b)\) What is the maximum acceleration of Alistair and Benedict?

\(\displaystyle c)\) Which of them reaches the surface of the water faster if they jump off the bridge at the same time?

We can assume that the elongation of the ropes is directly proportional to the stretching force. Ignore the height of the jumpers and air resistance.

(5 pont)

Deadline expired on June 17, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelöljük Aladár tömegét \(\displaystyle m_\mathrm{A}\)-val, rugalmas kötelének hosszát \(\displaystyle \ell_\mathrm{A}\)-val, és ennek a kötélnek megfelelő rugó direkciós állandóját (rugóállandóját) \(\displaystyle D_\mathrm{A}\)-val. A Bendegúzra vonatkozó megfelelő mennyiségek jele legyen \(\displaystyle m_\mathrm{B}\), \(\displaystyle \ell_\mathrm{B}\) és \(\displaystyle D_\mathrm{B}\). Az ugrás helyének a vízfelszíntől mért magasságát jelöljük \(\displaystyle h\)-val.

Az ismert adatok: \(\displaystyle m_\mathrm{A}=60\,\mathrm{kg}\),  \(\displaystyle m_\mathrm{B}=80\,\mathrm{kg}\),  \(\displaystyle D_\mathrm{A}=72\,\mathrm{N/m}\),  \(\displaystyle h=50\,\mathrm{m}\) és \(\displaystyle g=9{,}81\,\mathrm{m/s^2}\).

A keresett mennyiségek: \(\displaystyle \ell_\mathrm{A}\), \(\displaystyle \ell_\mathrm{B}\), \(\displaystyle D_\mathrm{B}\), illetve a két ugró maximális gyorsulása: \(\displaystyle a^\mathrm{max}_\mathrm{A}\) és \(\displaystyle a^\mathrm{max}_\mathrm{B}\).

\(\displaystyle a)\) Aladár kötelének hosszát legkönnyebben az energiamegmaradás tételének alkalmazásával kaphatjuk meg. Az elugráskor és a vízfelszínhez érkezéskor Aladár sebessége nulla, így csak a gravitációs helyzeti energia és a rugalmas energia változását kell figyelembe vennünk:

\(\displaystyle -m_\mathrm{A}gh+\frac{1}{2}D_\mathrm{A}\left(h-\ell_\mathrm{A}\right)^2=0,\)

ahonnan

\(\displaystyle \ell_\mathrm{A}=h-\sqrt{\frac{2m_\mathrm{A}gh}{D_\mathrm{A}}}=21{,}41\,\mathrm{m}\approx 21\,\mathrm{m}.\)

Hasonló megfontolással kapjuk meg Bendegúz rugalmas kötelének nyújtatlan hosszát. Az energiamegmaradás szerint

\(\displaystyle -m_\mathrm{B}gh+\frac{1}{2}D_\mathrm{B}\left(h-\ell_\mathrm{B}\right)^2=0.\)

Vegyük még figyelembe, hogy egy rugalmas kötél ,,rugóállandója'' függ a nyújtatlan kötél hosszától, annak reciprokával arányos. (Ez a Hooke-törvényből olvasható ki.) Ennek megfelelően

\(\displaystyle D_\mathrm{B}=D_\mathrm{A}\frac{\ell_\mathrm{A}}{\ell_\mathrm{B}},\)

tehát az energiatétel egyenlete:

\(\displaystyle m_\mathrm{B}gh=\frac{1}{2}D_\mathrm{A}\frac{\ell_\mathrm{A}}{\ell_\mathrm{B}}\left(h-\ell_\mathrm{B}\right)^2.\)

Ez \(\displaystyle \ell_\mathrm{B}\)-re nézve másodfokú egyenlet, amelynek \(\displaystyle h\)-nál kisebb megoldása:

\(\displaystyle \ell_\mathrm{B}=18{,}95\,\mathrm{m}\approx 19\,\mathrm{m}.\)

(Ennél pontosabb eredmény megadása az ugrók testmagasságának figyelembevétele nélkül értelmetlen lenne.)

Bendegúz kötelének direkciós állandója \(\displaystyle \ell_\mathrm{B}\) ismeretében már könnyen számolható:

\(\displaystyle D_\mathrm{B}\approx 81\,\mathrm{N/m}.\)

\(\displaystyle b)\) A legnagyobb (függőlegesen felfelé irányuló) gyorsulás a vízfelszínhez érés pillanatában következik be, hiszen ekkor a legnagyobb a kötelet feszítő erő. Newton törvénye szerint

\(\displaystyle m_\mathrm{A}a^\mathrm{max}_\mathrm{A}=D_\mathrm{A}\left(h-\ell_\mathrm{A}\right)-m_\mathrm{A}g,\)

ahonnan

\(\displaystyle a^\mathrm{max}_\mathrm{A}=\left(\sqrt{\frac{2D_\mathrm{A}h}{m_\mathrm{A}g}}-1\right)g\approx 2{,}5\,g.\)

Hasonló számolással adódik, hogy

\(\displaystyle a^\mathrm{max}_\mathrm{B}=\left(\sqrt{\frac{2D_\mathrm{B}h}{m_\mathrm{B}g}}-1\right)g\approx 2{,}2\,g.\)

A gyorsulás következtében az ugrást végző személy úgy érzi, mintha a nehézségi gyorsulás a megszokott \(\displaystyle g\)-ről \(\displaystyle g'=g+a^\mathrm{max}\) értékre növekedett volna. Aladár esetében \(\displaystyle g'\) legnagyobb értéke \(\displaystyle 3{,}5\,g\), Bendegúznál pedig \(\displaystyle 3{,}2\,g\). Érdekes, hogy a nagyobb tömegű, rövidebb kötélre kötött Bendegúz veséinek (és más belső szerveinek) ,,terhelése'' a kisebb, mint a kisebb tömegű, de hosszabb kötéllel rendelkező Aladár terhelése.

\(\displaystyle c)\) Az esési idők összehasonlítása első ránézésre nagyon nehéz kérdésnek tűnik, de nem az! Nincs szükség a két idő nagyságának pontos kiszámítására, hiszen csak az a kérdés, hogy melyik időtartam a rövidebb.

Számítsuk ki a ,,halálugrást'' végző személy sebességének négyzetét a megtett \(\displaystyle x\) út függvényében. Mindaddig, amíg a kötél laza, a mozgás szabadesés, tehát az \(\displaystyle x\le\ell\) szakaszon

\(\displaystyle v^2(x)=2g\cdot x.\)

A kötél fokozatos megfeszülése során (vagyis ha \(\displaystyle \ell<x\le h\)) az energiamegmaradás egyenlete szerint

\(\displaystyle \frac{1}{2}mv^2=mgx-\frac{1}{2}D(x-\ell)^2,\)

ahonnan

\(\displaystyle v^2(x)=2gx-\frac{D}{m}(x-\ell)^2.\)

A fenti képletekben \(\displaystyle m\), \(\displaystyle D\) és \(\displaystyle \ell\) helyébe Aladárnál és Bendegúznál a nekik megfelelő értékeket kell behelyettesítenünk. A paramétereket úgy állították be, hogy mindkét ugrónál \(\displaystyle v(x=h)=0\) teljesüljön.

Ábrázoljuk a \(\displaystyle v^2(x)\) függvény grafikonját. A képletekből leolvashatjuk, hogy a grafikon egy (az origóból induló, adott meredekségű) egyenesből és egy lefelé szélesedő parabolából tevődik össze. Mindkét görbe második zérushelye az \(\displaystyle x\) tengely \(\displaystyle x=h\) pontjánál van. Az egyenes és a parabola folytonosan és törésmentesen csatlakozik egymáshoz az \(\displaystyle x=\ell\) koordinátájú pontban.

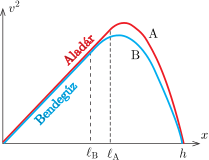
Az ábráról leolvashatjuk, hogy Bendegúz – kékkel jelölt – \(\displaystyle v^2\)-e sehol nem emelkedik Aladár piros görbéje fölé, és egy szakaszon pedig határozottan az alatt halad. Ugyanez érvényes a \(\displaystyle v(x)\) sebesség-út függvény grafikonjára is.

Ezek szerint a pálya bármely kicsiny \(\displaystyle \Delta x\) hosszúságú szakaszát Aladár nagyobb, vagy ugyanakkora sebességgel teszi meg, mint Bendegúz, emiatt biztosan hamarabb éri el a vízfelszínt, mint a nagyobb tömegű társa.

Statistics:

30 students sent a solution.
5 points:	Csiszár András, Csóka Péter, Czirják Márton Pál, Fehérvári Donát, Gerendás Roland, Hegedüs Márk, Klement Tamás, Rózsa Laura Enikő , Seprődi Barnabás Bendegúz, Szabó Donát, Tárnok Ede , Tóth Hanga Katalin, Zólomy Csanád Zsolt.
4 points:	Bélteki Teó, Debreceni Dániel, Dobos Anita, Kiss 131 Adorján Timon, Kovács Kristóf , Magyar Zsófia, Masa Barnabás, Tóth Kolos Barnabás, Žigo Boglárka.
3 points:	2 students.
1 point:	1 student.
0 point:	3 students.

Problems in Physics of KöMaL, May 2024