A P. 5574. feladat (2024. május)

P. 5574. Alul zárt, függőleges, hőszigetelt hengerben lévő dugattyúk azonos hőmérsékletű és térfogatú nitrogént zárnak el. Kezdetben a hőmérséklet $\displaystyle T_1=300~\mathrm{K}$. A felső dugattyú súrlódásmentesen mozoghat, a tömege $\displaystyle m=40~\mathrm{kg}$, az alsó jó hővezető anyagból készült és rögzített, a felső hőszigetelt. A külső légnyomás $\displaystyle 10^5~\mathrm{Pa}$, az alsó gáz nyomása $\displaystyle 1{,}2\cdot 10^5~\mathrm{Pa}$, a henger alapterülete $\displaystyle A=1~\mathrm{dm^2}$, $\displaystyle h=0{,}5~\mathrm{m}$.

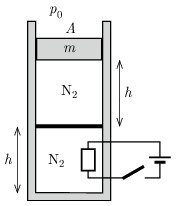
$\displaystyle a)$ Mennyi a felső és az alsó részben lévő nitrogén tömege?

A fűtőszál $\displaystyle Q=1580~\mathrm{J}$ hőt közöl a rendszerrel.

$\displaystyle b)$ Mennyivel változik meg a felső és az alsó gáz belső energiája?

$\displaystyle c)$ Mennyivel változik meg a felső gáz térfogata?

Közli: Veres Dénes, Szolnok

(4 pont)

A beküldési határidő 2024. június 17-én LEJÁRT.

Megoldás. $\displaystyle a)$ A felső részben lévő gáz térfogata $\displaystyle V_1=5\,\mathrm{dm^3}$, nyomása $\displaystyle p_1=10^5\,\mathrm{Pa}+\frac{40\,\mathrm{kg}\cdot9{,}81\mathrm{m/s^2}}{1\,\mathrm{dm^2}}=139\,\mathrm{kPa}$. Behelyettesítve az ideális gáz állapotegyenletébe, a felső részben lévő gáz anyagmennyiségére

$\displaystyle n_1=\frac{p_1V_1}{RT}=\frac{1{,}39\cdot10^5\,\mathrm{Pa}\cdot 0{,}005\,\mathrm{m^3}}{8{,}314\,\mathrm{\frac{J}{mol\cdot K}}\cdot 300\,\mathrm{K}}=0{,}279\,\mathrm{mol}$

adódik. A nitrogéngáz moláris tömege $\displaystyle 28\,\mathrm{\tfrac{g}{mol}}$, így a felső térrészben $\displaystyle 7{,}82\,\mathrm{g}$ gáz található. Az alsó térrészben a nitrogén anyagmennyisége

$\displaystyle n_2=\frac{1{,}2\cdot10^5\,\mathrm{Pa}\cdot0{,}005\,\mathrm{m^3}}{8{,}314\,\mathrm{\frac{J}{mol\cdot K}}\cdot 300\,\mathrm{K}}=0{,}241\,\mathrm{mol},$

melynek tömege $\displaystyle 6{,}74\,\mathrm{g}$.

$\displaystyle b)$ A melegítés hatására mindkét gáz hőmérséklete $\displaystyle \Delta T$ értékkel növekszik meg. Az alsó gáz állandó térfogaton történő melegítéséhez $\displaystyle \tfrac{f}{2}n_2R\Delta T$ hőmennyiség szükséges. A felső gáz izobár állapotváltozása során a felvett hő $\displaystyle \tfrac{f+2}{2}n_1R\Delta T$. A nitrogéngáz kétatomos molekulákból áll, így $\displaystyle f=5$. A fűtőszállal közölt összes hő ismeretében felírható, hogy

$\displaystyle \frac{f}{2}n_2R\Delta T+\frac{f+2}{2}n_1R\Delta T=1580\,\mathrm{J}.$

A hőmérséklet-növekedés értékére $\displaystyle \Delta T=120{,}4\,\mathrm{K}$ adódik. A belső energia növekedés a felső illetve alsó gázra:

$\displaystyle c)$ Gay-Lussac I. törvénye értelmében a végállapotban a felső gáz térfogata

$\displaystyle V_1'=V_1\frac{T_1+\Delta T}{T_1}=7{,}01\,\mathrm{dm^3}.$

A felső gáz térfogata $\displaystyle 2{,}01\,\mathrm{dm^3}$-rel növekedett meg a melegítés hatására.

Statisztika:

35 dolgozat érkezett.
4 pontot kapott:	Bélteki Teó, Csiszár András, Debreceni Dániel, Dobos Anita, Éliás Kristóf , Erős Fanni, Gerendás Roland, Hornok Máté, Kovács Kristóf , Masa Barnabás, Sütő Áron, Szabó Donát, Vágó Botond.
3 pontot kapott:	Fehérvári Donát, Fekete Lúcia, Kiss 131 Adorján Timon, Rózsa Laura Enikő , Tóth Hanga Katalin, Zólomy Csanád Zsolt.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2024. májusi fizika feladatai