 Problem P. 5575. (May 2024)
Problem P. 5575. (May 2024)
P. 5575. A small electric dipole is placed above a large grounded metal plate at a height of \(\displaystyle h\). This is done in such a way that its dipole moment \(\displaystyle \boldsymbol{p}\) points upwards as shown in the figure.
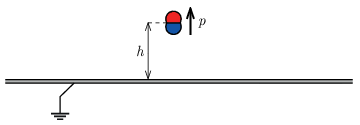
Determine the positions of the points on the metal sheet where the surface charge density is zero.
(5 pont)
Deadline expired on June 17, 2024.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Az elektromos dipólus modellezéséhez induljunk ki egy \(\displaystyle q\) és egy \(\displaystyle -q\) töltésből képzett párból, amelyek egymástól \(\displaystyle d\) távolságra helyezkednek el. Ha elvégezzük a \(\displaystyle d\to 0\), \(\displaystyle q\to\infty\) határértékeket a \(\displaystyle p=qd\) konstans feltétel mellett, akkor megkapjuk az ideális dipólust.
Vizsgáljuk meg, hogy mi történik a tükörtöltésekkel a határérték elvégzése közben! A \(\displaystyle q\) illetve \(\displaystyle -q\) töltésekhez rendre \(\displaystyle -q\) illetve \(\displaystyle q\) tükörtöltések tartoznak, amelyek egymástól vett távolsága \(\displaystyle d\). Mivel a töltések előjele felcserélődik, az említett limeszben könnyen látható, hogy a tükördipólus a valódival párhuzamos \(\displaystyle \boldsymbol{p}\) dipólmomentummal jellemezhető.
Az elektromos térerősség értéke a koordináta-rendszer \(\displaystyle (x,y)\) síkjába helyezett fémlap felületén, az elrendezés szimmetriatengelyétől \(\displaystyle r\) távolságra a valódi és tükördipólusok járulékainak összegeként adódik:
\(\displaystyle \boldsymbol{E}(r)=\frac{1}{2\pi\varepsilon_0}\frac{3ph^2-p(h^2+r^2)}{(h^2+r^2)^{5/2}}\begin{pmatrix}0\\0\\1\end{pmatrix},\)
ez a várakozásainknak megfelelően merőleges a fémlapra. A felületi töltéssűrűség a \(\displaystyle \sigma=\varepsilon_0 E\) összefüggésből kapható:
\(\displaystyle \sigma(r)=\frac{p}{2\pi}\frac{2h^2-r^2}{(h^2+r^2)^{5/2}}.\)
Jól látható, hogy a fenti kifejezés számlálója zérussá válik, amennyiben a \(\displaystyle r\) sugár az alábbi \(\displaystyle R\) értéket veszi fel:
\(\displaystyle R=\sqrt{2}\,h.\)
A töltéssűrűség tehát egy ekkora sugarú körvonal mentén zérus.
II. megoldás. A fémlap közvetlen közelében az elektromos térerősség merőleges a fémlapra, nagysága helyről helyre változó \(\displaystyle E_\perp\). A fémlap felületi töltéssűrűsége (egységnyi felületen található töltés nagysága) a Gauss-féle fluxustörvény szerint arányos az \(\displaystyle E_\perp\) komponenssel, tehát ott válik nullává, ahol \(\displaystyle E_\perp\) eltűnik.
A fémlapnak a dipólust tartalmazó oldalán az elektromos térerősség úgy számítható ki, mintha a fémlap ott se lenne. Helyette a ténylegesen ott lévő (az alábbi ábrákon pirosan jelölt) dipólus mellett egy, annak a fémlapra vett tükörkép-pontjában található másik, ugyancsak \(\displaystyle \boldsymbol p\) dipólmomentummal rendelkező (kék színnel jelölt) ,,tükördipólus'' elektromos terét is számításba kell vegyük. (Ez a tükrözési módszer az elektrosztatikában.)
Megjegyzés. Érdekes, hogy a tükördipól iránya nem tükröződik, hanem \(\displaystyle \boldsymbol{p}\)-vel megegyező marad. Ennek az a szemléletes magyarázata, hogy a tükrözés során a dipólust alkotó két, egymáshoz közeli töltést összekötő vektor iránya is és a töltések előjele is megváltozik, a szorzatuk tehát változatlan marad.
Egyetlen elektromos dipólus térerőssége a dipólus helyétől \(\displaystyle \boldsymbol{r}\) vektorral megadott pontban
\(\displaystyle \boldsymbol{E}(\boldsymbol{r})=\frac{1}{4\pi\varepsilon_0}\frac{(3\boldsymbol{p}\boldsymbol{r})\boldsymbol{r}-\boldsymbol{p}r^2}{r^5}.\)
(Ez a formula tankönyvekben és az interneten is megtalálható.)
Esetünkben a teljes elektromos térerősség a valódi és a tükördipólus terének összege:
\(\displaystyle \boldsymbol{E}=\frac{1}{4\pi\varepsilon_0}\left(\frac{(3\boldsymbol{p}\boldsymbol{r})\boldsymbol{r}-\boldsymbol{p}r^2}{r^5} +\frac{(3\boldsymbol{p}\boldsymbol{r'})\boldsymbol{r'}-\boldsymbol{p}r'^2}{r'^5}\right),\)
ahol \(\displaystyle \boldsymbol{r'}\) a tükördipólustól a vizsgált pontba mutató vektor (1. ábra). Az ábráról leolvasható, hogy \(\displaystyle \vert\boldsymbol{r'}\vert\equiv r'=r.\)
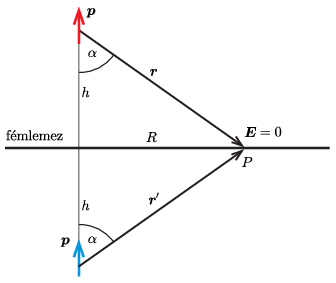
1. ábra
A fenti térerősségnek a normális irányú (a fémlapra merőleges) komponense akkor nulla, ha \(\displaystyle \boldsymbol{E}\)-t egy normális irányú vektorral, például \(\displaystyle \boldsymbol{p}\)-vel skalárisan szorozva nullát kapunk: \(\displaystyle \boldsymbol{E}\cdot\boldsymbol{p}=0\). Ez akkor teljesül, ha
\(\displaystyle 3(\boldsymbol{p}\boldsymbol{r})^2+3(\boldsymbol{p}\boldsymbol{r'})^2-2p^2r^2=0.\)
Tekintettel arra, hogy \(\displaystyle \boldsymbol{p}\) merőleges az \(\displaystyle \boldsymbol{r}+\boldsymbol{r'}\) vektorra, vagyis \(\displaystyle \boldsymbol{p}\left(\boldsymbol{r}+\boldsymbol{r'}\right)=0,\) így
\(\displaystyle \boldsymbol{p}\boldsymbol{r}=-\boldsymbol{p}\boldsymbol{r'}\qquad \text{és}\qquad (\boldsymbol{p}\boldsymbol{r})^2=(-\boldsymbol{p}\boldsymbol{r'})^2=p^2r^2\cos^2\alpha.\)
A felületi töltéssűrűség eltűnésének feltétele (behelyettesítés és 2-vel való osztás után):
\(\displaystyle 3p^2r^2\cos^2\alpha=p^2r^2,\)
azaz \(\displaystyle \cos\alpha=\frac{1}{\sqrt3}\). Innen a kérdéses távolság
\(\displaystyle R=h\tg\alpha=\sqrt{2}\,h,\)
vagyis a fémfelület töltéssűrűsége egy \(\displaystyle R\) sugarú kör mentén válik zérussá.
III. megoldás. Gauss sokat foglalkozott a mágneses dipólusok által keltett mágneses mező sajátságaival. Megállapította, hogy egy \(\displaystyle \boldsymbol{m}\) erősségű mágneses dipólus tengelye mentén, attól \(\displaystyle r\) távolságban a mágneses tér (mai szóhasználattal: a mágneses indukció) \(\displaystyle \boldsymbol{m}\) irányú és \(\displaystyle 2k\frac{m}{r^3}\) nagyságú. Az arányossági tényező a mértékegységek választásától függ, Gauss például \(\displaystyle k\)-t 1-nek vette; SI egységekben pedig \(\displaystyle k=\mu_0/(4\pi)\). Gauss azt is megállapította, hogy a dipólus tengelyére merőleges irányban a mágneses indukció \(\displaystyle \boldsymbol{m}\)-mel ellentétes irányú és \(\displaystyle k\frac{m}{r^3}\) nagyságú. Ezt a két irányt (vagyis amikor \(\displaystyle \boldsymbol{r}\) párhuzamos, illetve merőleges \(\displaystyle \boldsymbol{m}\)-re) Gauss-féle I. és II. főhelyzetnek nevezik.
Az elektromos dipólusok által keltett elektromos tér a főhelyzetekben a mágneses térrel analóg összefüggésekkel írható le. Bontsuk fel \(\displaystyle \boldsymbol{p}\)-t két olyan vektor összegére, amelyeknek a keresett \(\displaystyle P\) pont a Gauss-féle I., illetve II. főhelyzetébe kerül, és járjunk el ugyanígy a tükördipólus esetében is (2. ábra).
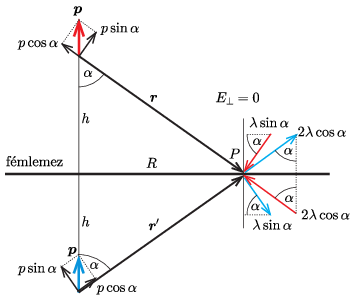
2. ábra
Az egyes dipóluskomponensek nagysága \(\displaystyle p\cos\alpha\) és \(\displaystyle p\sin\alpha\), és a \(\displaystyle P\) pont mindegyik dipól-összetevőtől ugyanakkora \(\displaystyle r\) távolságban van. Ennek megfelelően az eredő elektromos térerősség a fémlemez \(\displaystyle P\) pontjánál – a szuperpozíció-elvnek megfelelően – a négy járulék összege
\(\displaystyle 2\lambda\cos^2\alpha-\lambda\sin^2\alpha+2\lambda\cos^2\alpha-\lambda\sin^2\alpha=0.\)
(A \(\displaystyle \lambda\) állandó a fentebb említett \(\displaystyle k\) konstans elektrosztatikus megfelelőjének és a mindegyik dipól-összetevőre ugyanakkora \(\displaystyle p/r^3\) tényezőnek a szorzata.) A nulla töltéssűrűségű helyeket tehát a \(\displaystyle 4\cos^2\alpha=2\sin^2\alpha\) egyenlet jellemzi, ahonnan
\(\displaystyle \tg\alpha=\sqrt2,\qquad\text{és így}\qquad R=\sqrt2\,h.\)
Statistics:
12 students sent a solution. 5 points: Csóka Péter, Czirják Márton Pál, Gerendás Roland, Kiss 131 Adorján Timon, Pázmándi József Áron, Seprődi Barnabás Bendegúz. 4 points: Dobos Anita, Tóth Kolos Barnabás. 1 point: 3 students.
Problems in Physics of KöMaL, May 2024
