 |
A P. 5575. feladat (2024. május) |
P. 5575. Nagy méretű, földelt fémlap felett h magasságban egy kicsiny elektromos dipólust helyezünk el. Mindezt úgy tesszük, hogy annak \displaystyle \boldsymbol{p} dipólmomentuma az ábrán látott módon felfelé mutasson.
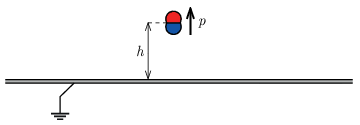
Határozzuk meg a fémlapon azon pontok helyét, ahol a felületi töltéssűrűség zérus!
Közli: Németh Róbert, Budapest
(5 pont)
A beküldési határidő 2024. június 17-én LEJÁRT.
I. megoldás. Az elektromos dipólus modellezéséhez induljunk ki egy \displaystyle q és egy \displaystyle -q töltésből képzett párból, amelyek egymástól \displaystyle d távolságra helyezkednek el. Ha elvégezzük a \displaystyle d\to 0, \displaystyle q\to\infty határértékeket a \displaystyle p=qd konstans feltétel mellett, akkor megkapjuk az ideális dipólust.
Vizsgáljuk meg, hogy mi történik a tükörtöltésekkel a határérték elvégzése közben! A \displaystyle q illetve \displaystyle -q töltésekhez rendre \displaystyle -q illetve \displaystyle q tükörtöltések tartoznak, amelyek egymástól vett távolsága \displaystyle d. Mivel a töltések előjele felcserélődik, az említett limeszben könnyen látható, hogy a tükördipólus a valódival párhuzamos \displaystyle \boldsymbol{p} dipólmomentummal jellemezhető.
Az elektromos térerősség értéke a koordináta-rendszer \displaystyle (x,y) síkjába helyezett fémlap felületén, az elrendezés szimmetriatengelyétől \displaystyle r távolságra a valódi és tükördipólusok járulékainak összegeként adódik:
\displaystyle \boldsymbol{E}(r)=\frac{1}{2\pi\varepsilon_0}\frac{3ph^2-p(h^2+r^2)}{(h^2+r^2)^{5/2}}\begin{pmatrix}0\\0\\1\end{pmatrix},
ez a várakozásainknak megfelelően merőleges a fémlapra. A felületi töltéssűrűség a \displaystyle \sigma=\varepsilon_0 E összefüggésből kapható:
\displaystyle \sigma(r)=\frac{p}{2\pi}\frac{2h^2-r^2}{(h^2+r^2)^{5/2}}.
Jól látható, hogy a fenti kifejezés számlálója zérussá válik, amennyiben a \displaystyle r sugár az alábbi \displaystyle R értéket veszi fel:
\displaystyle R=\sqrt{2}\,h.
A töltéssűrűség tehát egy ekkora sugarú körvonal mentén zérus.
II. megoldás. A fémlap közvetlen közelében az elektromos térerősség merőleges a fémlapra, nagysága helyről helyre változó \displaystyle E_\perp. A fémlap felületi töltéssűrűsége (egységnyi felületen található töltés nagysága) a Gauss-féle fluxustörvény szerint arányos az \displaystyle E_\perp komponenssel, tehát ott válik nullává, ahol \displaystyle E_\perp eltűnik.
A fémlapnak a dipólust tartalmazó oldalán az elektromos térerősség úgy számítható ki, mintha a fémlap ott se lenne. Helyette a ténylegesen ott lévő (az alábbi ábrákon pirosan jelölt) dipólus mellett egy, annak a fémlapra vett tükörkép-pontjában található másik, ugyancsak \displaystyle \boldsymbol p dipólmomentummal rendelkező (kék színnel jelölt) ,,tükördipólus'' elektromos terét is számításba kell vegyük. (Ez a tükrözési módszer az elektrosztatikában.)
Megjegyzés. Érdekes, hogy a tükördipól iránya nem tükröződik, hanem \displaystyle \boldsymbol{p}-vel megegyező marad. Ennek az a szemléletes magyarázata, hogy a tükrözés során a dipólust alkotó két, egymáshoz közeli töltést összekötő vektor iránya is és a töltések előjele is megváltozik, a szorzatuk tehát változatlan marad.
Egyetlen elektromos dipólus térerőssége a dipólus helyétől \displaystyle \boldsymbol{r} vektorral megadott pontban
\displaystyle \boldsymbol{E}(\boldsymbol{r})=\frac{1}{4\pi\varepsilon_0}\frac{(3\boldsymbol{p}\boldsymbol{r})\boldsymbol{r}-\boldsymbol{p}r^2}{r^5}.
(Ez a formula tankönyvekben és az interneten is megtalálható.)
Esetünkben a teljes elektromos térerősség a valódi és a tükördipólus terének összege:
\displaystyle \boldsymbol{E}=\frac{1}{4\pi\varepsilon_0}\left(\frac{(3\boldsymbol{p}\boldsymbol{r})\boldsymbol{r}-\boldsymbol{p}r^2}{r^5} +\frac{(3\boldsymbol{p}\boldsymbol{r'})\boldsymbol{r'}-\boldsymbol{p}r'^2}{r'^5}\right),
ahol \displaystyle \boldsymbol{r'} a tükördipólustól a vizsgált pontba mutató vektor (1. ábra). Az ábráról leolvasható, hogy \displaystyle \vert\boldsymbol{r'}\vert\equiv r'=r.
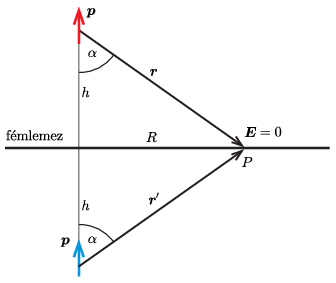
1. ábra
A fenti térerősségnek a normális irányú (a fémlapra merőleges) komponense akkor nulla, ha \displaystyle \boldsymbol{E}-t egy normális irányú vektorral, például \displaystyle \boldsymbol{p}-vel skalárisan szorozva nullát kapunk: \displaystyle \boldsymbol{E}\cdot\boldsymbol{p}=0. Ez akkor teljesül, ha
\displaystyle 3(\boldsymbol{p}\boldsymbol{r})^2+3(\boldsymbol{p}\boldsymbol{r'})^2-2p^2r^2=0.
Tekintettel arra, hogy \displaystyle \boldsymbol{p} merőleges az \displaystyle \boldsymbol{r}+\boldsymbol{r'} vektorra, vagyis \displaystyle \boldsymbol{p}\left(\boldsymbol{r}+\boldsymbol{r'}\right)=0, így
\displaystyle \boldsymbol{p}\boldsymbol{r}=-\boldsymbol{p}\boldsymbol{r'}\qquad \text{és}\qquad (\boldsymbol{p}\boldsymbol{r})^2=(-\boldsymbol{p}\boldsymbol{r'})^2=p^2r^2\cos^2\alpha.
A felületi töltéssűrűség eltűnésének feltétele (behelyettesítés és 2-vel való osztás után):
\displaystyle 3p^2r^2\cos^2\alpha=p^2r^2,
azaz \displaystyle \cos\alpha=\frac{1}{\sqrt3}. Innen a kérdéses távolság
\displaystyle R=h\tg\alpha=\sqrt{2}\,h,
vagyis a fémfelület töltéssűrűsége egy \displaystyle R sugarú kör mentén válik zérussá.
III. megoldás. Gauss sokat foglalkozott a mágneses dipólusok által keltett mágneses mező sajátságaival. Megállapította, hogy egy \displaystyle \boldsymbol{m} erősségű mágneses dipólus tengelye mentén, attól \displaystyle r távolságban a mágneses tér (mai szóhasználattal: a mágneses indukció) \displaystyle \boldsymbol{m} irányú és \displaystyle 2k\frac{m}{r^3} nagyságú. Az arányossági tényező a mértékegységek választásától függ, Gauss például \displaystyle k-t 1-nek vette; SI egységekben pedig \displaystyle k=\mu_0/(4\pi). Gauss azt is megállapította, hogy a dipólus tengelyére merőleges irányban a mágneses indukció \displaystyle \boldsymbol{m}-mel ellentétes irányú és \displaystyle k\frac{m}{r^3} nagyságú. Ezt a két irányt (vagyis amikor \displaystyle \boldsymbol{r} párhuzamos, illetve merőleges \displaystyle \boldsymbol{m}-re) Gauss-féle I. és II. főhelyzetnek nevezik.
Az elektromos dipólusok által keltett elektromos tér a főhelyzetekben a mágneses térrel analóg összefüggésekkel írható le. Bontsuk fel \displaystyle \boldsymbol{p}-t két olyan vektor összegére, amelyeknek a keresett \displaystyle P pont a Gauss-féle I., illetve II. főhelyzetébe kerül, és járjunk el ugyanígy a tükördipólus esetében is (2. ábra).
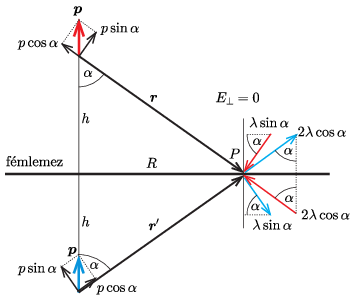
2. ábra
Az egyes dipóluskomponensek nagysága \displaystyle p\cos\alpha és \displaystyle p\sin\alpha, és a \displaystyle P pont mindegyik dipól-összetevőtől ugyanakkora \displaystyle r távolságban van. Ennek megfelelően az eredő elektromos térerősség a fémlemez \displaystyle P pontjánál – a szuperpozíció-elvnek megfelelően – a négy járulék összege
\displaystyle 2\lambda\cos^2\alpha-\lambda\sin^2\alpha+2\lambda\cos^2\alpha-\lambda\sin^2\alpha=0.
(A \displaystyle \lambda állandó a fentebb említett \displaystyle k konstans elektrosztatikus megfelelőjének és a mindegyik dipól-összetevőre ugyanakkora \displaystyle p/r^3 tényezőnek a szorzata.) A nulla töltéssűrűségű helyeket tehát a \displaystyle 4\cos^2\alpha=2\sin^2\alpha egyenlet jellemzi, ahonnan
\displaystyle \tg\alpha=\sqrt2,\qquad\text{és így}\qquad R=\sqrt2\,h.
Statisztika:
12 dolgozat érkezett. 5 pontot kapott: Csóka Péter, Czirják Márton Pál, Gerendás Roland, Kiss 131 Adorján Timon, Pázmándi József Áron, Seprődi Barnabás Bendegúz. 4 pontot kapott: Dobos Anita, Tóth Kolos Barnabás. 1 pontot kapott: 3 versenyző.
A KöMaL 2024. májusi fizika feladatai
|
|

