 |
A P. 5576. feladat (2024. május) |
P. 5576. Tegyük fel, hogy rendelkezünk olyan mérőműszerekkel, amelyek nemcsak szinuszos váltóáram, illetve váltófeszültség effektív értékét mérik, hanem tetszőleges periodikus jelekét is.
\(\displaystyle a)\) Csatlakoztassunk egy \(\displaystyle f=1/T\) frekvenciájú, szimmetrikus négyszögjelet szolgáltató feszültséggenerátorra egy ideális induktivitást, amelynek önindukciós együtthatója \(\displaystyle L\). Ideális feszültség- és árammérő műszerekkel megmérjük az induktivitás áramának effektív értékét, illetve a feszültséggenerátor feszültségének effektív értékét. Mit mutatnak a műszerek, ha a négyszögjel lefutását a következő ábra mutatja, továbbá tudjuk, hogy a \(\displaystyle t=0\) időpillanatban az induktivitás árama zérus?
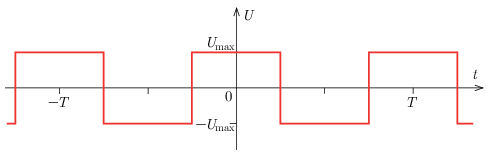
\(\displaystyle b)\) Csatlakoztassunk egy \(\displaystyle f=1/T\) frekvenciájú, szimmetrikus négyszögjelet szolgáltató áramgenerátorra egy ideális kondenzátort, amelynek kapacitása \(\displaystyle C\). Ideális feszültség- és árammérő műszerekkel megmérjük a kondenzátor áramának effektív értékét, illetve a áramgenerátor kimeneti feszültségének effektív értékét. Mit mutatnak a műszerek, ha a négyszögjel lefutását a következő ábra mutatja, továbbá tudjuk, hogy a kondenzátor feszültsége a \(\displaystyle t=0\) időpillanatban zérus?
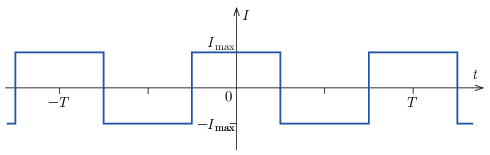
Mit mutatnak a műszerek az \(\displaystyle a)\) és a \(\displaystyle b)\) esetben? A válaszokat \(\displaystyle I_\mathrm{max}\), \(\displaystyle U_\mathrm{max}\), \(\displaystyle L\), \(\displaystyle C\) és \(\displaystyle f\) segítségével adjuk meg.
Közli: Honyek Gyula, Veresegyház
(5 pont)
A beküldési határidő 2024. június 17-én LEJÁRT.
Megoldás. Az effektív érték a négyzetérték időátlagából vont gyöknek felel meg. Az \(\displaystyle a)\) esetben a feszültséggenerátor, a \(\displaystyle b)\) esetben pedig az áramgenerátor négyszögjeleket produkál, melyeknek a négyzete időben állandó, tehát ezek esetében a műszerek egyszerűen \(\displaystyle U_{\mathrm{max}}\), illetve \(\displaystyle I_{\mathrm{max}}\) értékeket fognak mutatni.
\(\displaystyle a)\) Az ideális induktivitásra kapcsolt állandó feszültség időben lineárisan változó áramot hoz létre az \(\displaystyle U=L\frac{\Delta I}{\Delta t}\) összefüggés alapján. Esetünkben ez az áramerősség-idő függvény a \(\displaystyle 0\le t\le\tfrac{T}{4}\) intervallumban:
\(\displaystyle I(t)=\frac{U_{\mathrm{max}}}{L}t.\)
A periodikusan \(\displaystyle +U_{\mathrm{max}}\) és \(\displaystyle -U_{\mathrm{max}}\) között váltakozó feszültség hatására kialakuló áramerősség, illetve az áramerősség négyzetének időfüggését a következő grafikon mutatja:
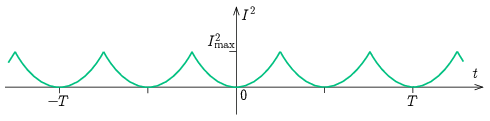
A fentiek alapján láthatjuk, hogy
\(\displaystyle I_{\mathrm{max}}=\frac{U_{\mathrm{max}}}{L}\frac{T}{4}=\frac{U_{\mathrm{max}}}{4Lf},\)
illetve
\(\displaystyle I_{\mathrm{max}}^2=\frac{U_{\mathrm{max}}^2}{L^2}\frac{T^2}{16}=\frac{U_{\mathrm{max}}^2}{16L^2f^2}.\)
Közismert, hogy az \(\displaystyle y=x^2\) függvény görbe alatti területe a \(\displaystyle [0,1]\) intervallumban \(\displaystyle \tfrac{1}{3}\), így a grafikonokon látható periodikus áram effektív értéke:
\(\displaystyle I_\mathrm{eff}=\frac{I_\mathrm{max}}{\sqrt{3}}=\frac{U_{\mathrm{max}}}{4\sqrt{3}Lf}.\)
\(\displaystyle b)\) Az előzőekhez nagyon hasonló a kondenzátor viselkedése, ha a fegyverzetére négyszögjelet produkáló áramgenerátort kapcsolunk. A kondenzátor töltése a \(\displaystyle 0\le t\le\tfrac{T}{4}\) időintervallumban lineárisan növekszik: \(\displaystyle Q(t)=I_\mathrm{max}t\), és ekkor a fegyverzetein mérhető feszültség
\(\displaystyle U(t)=\frac{Q(t)}{C}=\frac{I_\mathrm{max}}{C}t\)
lesz. A feszültség-idő grafikon az origóra szimmetrikus háromszögjel lesz, ami teljesen hasonló, mint az \(\displaystyle a)\) részben tárgyalt áram-idő grafikon.
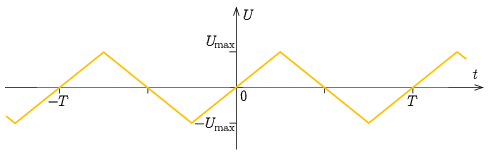
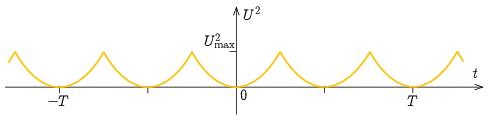
A feszültség maximális értéke
\(\displaystyle U_\mathrm{max}=\frac{I_\mathrm{max}}{C}\frac{T}{4}=\frac{I_\mathrm{max}}{4Cf},\)
és végül a feszültség effektív értéke:
\(\displaystyle U_\mathrm{eff}=\frac{U_\mathrm{max}}{\sqrt{3}}=\frac{I_{\mathrm{max}}}{4\sqrt{3}Cf}.\)
Statisztika:
9 dolgozat érkezett. 5 pontot kapott: Czirják Márton Pál, Debreceni Dániel, Hegedüs Márk, Klement Tamás, Szabó Donát. 4 pontot kapott: Dobos Anita, Tóth Kolos Barnabás. 3 pontot kapott: 1 versenyző.
A KöMaL 2024. májusi fizika feladatai