A P. 5579. feladat (2024. május)

P. 5579. Helsinkiben karácsonykor kicsit több mint 6 és fél perc alatt kel fel a Nap. Mikor lesz ugyanott az év során a legrövidebb ez az időtartam? Hány percig tart Helsinkiben a leggyorsabb napfelkelte?

Helsinki az északi szélesség 60. fokán fekszik, sík területen. A Nap látszólagos átmérője körülbelül fél fok. A földpálya excentricitásából származó kicsiny eltérésekkel és a légkör hatásával ebben a feladatban ne foglalkozzunk.

Közli: Vankó Péter, Budapest

(6 pont)

A beküldési határidő 2024. június 17-én LEJÁRT.

I. megoldás. Tekintsük a Földet a keringési síkjában a Nap-Föld tengelyre merőleges irányból. A Föld felületének egyik oldaláról a teljes Nap látszik, a másik oldalról nézve a teljes Nap a horizont alatt van. A két részt (a Föld sugarát \(\displaystyle R\)-rel jelölve) egy a Nap \(\displaystyle \Delta\eta\) látószögével egyenlő középponti szöggel jellemezhető, szimmetrikusan elhelyezkedő

\(\displaystyle d=\Delta\eta\,R\)

szélességű sáv (gömböv) választja el egymástól, amelyből a Nap egy része látszik csak. A felszín egy adott pontján addig tart a napfelkelte (napnyugta), amíg az adott pont ezen a sávon áthalad. Ha eltekintünk a pályamenti mozgástól, a forgásból adódó sebesség minden pontban időben állandó, így a napfelkelte ideje akkor a legrövidebb, ha a pont ezen a sávon merőlegesen halad át. Ez akkor van, ha a forgástengely merőleges a Nap-Föld tengelyre, azaz vagy a tavaszi, vagy az őszi nap-éj egyenlőségkor. A \(\displaystyle \varphi\) szélességi kör pontjainak a sebessége (a Föld lapultságát figyelmen kívül hagyva)

\(\displaystyle v=\frac{2\pi R\cos\varphi}{T},\)

ahol \(\displaystyle T\) a forgás periódusa, azaz egy nap. Mindebből a napfelkelte időtartama

\(\displaystyle \Delta t=\frac{d}{v}=\frac{\Delta\eta}{2\pi}\frac{1}{\cos\varphi}T\)

Adatainkkal (\(\displaystyle \Delta\eta=0{,}5^{\circ}=\tfrac{0{,}5}{360}2\pi\), \(\displaystyle \varphi=60^{\circ}\)) \(\displaystyle \Delta t=4\) percet kapunk.

Megjegyzés. Abból, hogy a nap-éj egyenlőség idején a földfelszín minden pontja merőlegesen halad át a ,,napfelkelte (napnyugta) sávon", nem következik, hogy ilyenkor a Nap függőlegesen emelkedik a horizont fölé (vagy süllyed az alá). A Nap látszólagos útjának a horizonttal bezárt szögét az határozza meg, hogy földfelszín minden, – az egyenlítőtől különböző – pontjában maga a horizont is forog \(\displaystyle \omega \sin \varphi=(360^{\circ}/\mathrm{nap})\sin\varphi\) szögsebességgel. (Ez a szögsebesség a Föld szögsebesség vektorának az adott ponthoz tartozó horizont síkjára merőleges komponense.)

Ezzel a feladatban feltett kérdést megválaszoltuk, a továbbiakban a probléma teljesebb leírása szerepel.

Ebben a közelítésben (amikor tehát elhanyagoltuk a Föld lapultságát, a keringését a Nap körül, és a légkör hatását) a napfelkelte és napnyugta hossza viszonylag könnyen kiszámítható az év bármely napjára. Elsőként rögzítsük a viszonyítási rendszereket! Legyen az \(\displaystyle x\) tengely a Nap-Föld tengely meghosszabbítása a sötét oldalon, az \(\displaystyle y\) tengely erre merőleges a keringés síkjában, és a \(\displaystyle z\) pedig mindkettőre merőleges! Ebben a rendszerben a ,,napkelte-napnyugta'' sáv a Föld felszínének és az \(\displaystyle S_\pm: x=\pm d/2\) síkoknak a metszetei által határolt gömböv. A forgástengely helyzetét adjuk meg gömbi polár koordináták segítségével: a \(\displaystyle \theta\) polárszöget (ami a Föld-tengely esetében mindig 23,5\(\displaystyle ^\circ\) ) mérjük a \(\displaystyle z\), a \(\displaystyle \psi\) azimutot pedig az \(\displaystyle x\) tengelytől! Így a forgástengely irányát megadó \(\displaystyle \mathbf{e}(\psi,\theta)\) egységvektor

\(\displaystyle \mathbf{e}(\psi,\theta)=\begin{pmatrix}\cos\psi\sin\theta\\ \sin\psi\sin\theta\\ \cos\theta\end{pmatrix}.\)

Ebből megállapítható az Egyenlítő (és így bármelyik szélességi kör) síkjának az \(\displaystyle S_\pm\) síkokkal bezárt \(\displaystyle \alpha\) szöge. Ez azonos a kérdéses síkok normálisainak, azaz a forgástengelynek és az \(\displaystyle x\) tengelynek a szögével, aminek a koszinusza éppen az \(\displaystyle \mathbf{e}(\psi,\theta)\) \(\displaystyle x\) komponense:

\(\displaystyle \cos\alpha=\cos\psi\sin\theta\)

A konstrukcióból következően \(\displaystyle \alpha\) a Nap iránya és az Egyenlítő síkja által bezárt \(\displaystyle -\phi\) szög pótszöge, \(\displaystyle \cos\psi\sin\theta=\cos\alpha=-\sin\phi\). (Itt azt a konvenciót követjük, hogy \(\displaystyle \phi\) pozitív, ha a Nap az Egyenlítő ,,fölött'', és negatív, ha az ,,alatt'' van. Az ábra egy téli helyzetet mutat, ilyenkor \(\displaystyle \alpha<\pi/2\), és \(\displaystyle \phi<0\). Ebben a konvencióban az \(\displaystyle \alpha-\phi=\pi/2\) összefüggés igaz nyáron is, amikor \(\displaystyle \alpha>\pi/2\) tehát formálisan nincs pótszöge.)

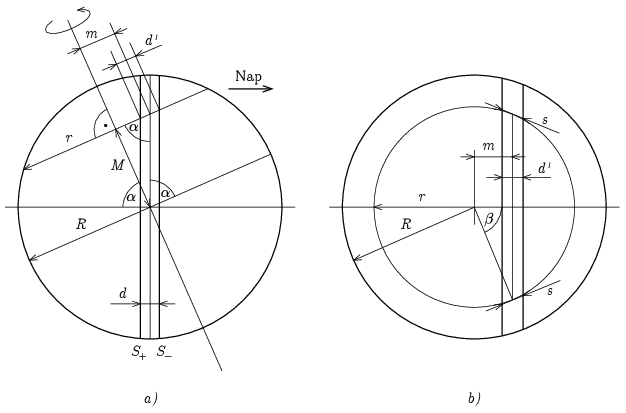
1. ábra

Az 1/a ábra azt a síkmetszetet mutatja, amely merőleges az \(\displaystyle S_\pm\) síkokra, a szélességi körökre, és magába foglalja a Föld forgástengelyét (tehát nem a fentiekben definiált \(\displaystyle x\)-\(\displaystyle z\) sík!), míg az 1/b ábra a \(\displaystyle \varphi\) szélességi kört tartalmazó, (az 1/a ábra síkjára) merőleges metszet látható. (Az ábra torz különösen az \(\displaystyle S_\pm\) síkok \(\displaystyle d\) távolságát illetően, ez ugyanis minden más távolságnál lényegesen kisebb, arányos ábrán nem lehetne a két síkot megkülönböztetni.) Ezekről leolvasható, hogy az \(\displaystyle S_\pm\) síkok a \(\displaystyle \varphi\) szélességhez tartozó síkot két egymástól

\(\displaystyle d'=\frac{d}{\sin\alpha}\)

távolságban futó, a középponttól

\(\displaystyle m=\frac{M}{\tg\alpha}\pm\frac{d'}{2}\simeq\frac{M}{\tg\alpha}\)

távolságra lévő párhuzamos egyenesben metszik, ahol

\(\displaystyle M=R\sin\varphi.\)

Látható az is, hogy a kérdéses szélességi körnek jó esetben két,

\(\displaystyle s=\frac{d'}{\sin\beta}\)

hosszúságú szakasza esik a két sík közé, ahol

\(\displaystyle \cos\beta=\frac{m}{r}.\)

Az eddigieket összegezve tehát a \(\displaystyle \varphi\)-vel jellemzett szélességi körnek két, egyenként

\(\displaystyle s=\frac{R\Delta\eta}{\sqrt{\sin^2{\alpha}-{\tg}^2\varphi\cos^2\alpha}}\)

hosszúságú darabja (íve) esik az \(\displaystyle S_\pm\) síkok közé, ezek felelnek meg a napfelkeltének és a napnyugtának. A szélességi kör egyes pontjai ezeken

\(\displaystyle \Delta t=\frac{s}{v}=\frac{T\Delta\eta}{2\pi\cos\varphi\sqrt{\sin^2\alpha-\tg^2\varphi\cos^2\alpha}}= \frac{T\Delta\eta}{2\pi}\frac{1}{\sqrt{\cos^2\varphi-\sin^2\theta\cos^2\psi}}=\frac{T\Delta\eta}{2\pi}\frac{1}{\sqrt{\cos^2\varphi-\sin^2\phi}}\)

idő alatt haladnak végig.

Az általunk felvett \(\displaystyle (x,y,z)\) koordináta-rendszer egy év periódussal forog a \(\displaystyle z\) tengely körül, ennek megfelelően a \(\displaystyle \psi\) ,,visszafelé'' forog, egy év alatt összesen \(\displaystyle -2\pi\)-t változik. Ha pl. \(\displaystyle \delta\)-val jelöljük a Föld pályáján való előrehaladásának a szögét a nyári napfordulótól mérve, akkor \(\displaystyle \psi=\pi-\delta\). Így a téli napforduló idején \(\displaystyle 0\), a tavaszi és őszi nap-éj egyenlőségkor pedig \(\displaystyle \pm\pi/2\) értékű. Ez utóbbiak adják a napkelte ill. napnyugta hosszának a szélsőérték helyeit. (Az ábra egy téli helyzetet mutat.) Látható, a kifejezésünk csak addig értelmes, amíg

\(\displaystyle \left\vert\cos\varphi\right\vert>\left\vert\sin\theta\cos\psi\right\vert.\)

Ennek nyilvánvaló oka, hogy a sarkkörön (\(\displaystyle \varphi=\pi/2-\theta\)) túl az év bizonyos részeiben nem megy le, illetve nem kel fel a Nap.

Megjegyzés. Képletünk megbízhatatlanná válik, ha

\(\displaystyle \left\vert\cos\varphi\right\vert\gtrapprox\left\vert\sin\theta\cos\psi\right\vert.\)

Ha ugyanis az adott szélességi kör túl kicsiny szög alatt metszi az \(\displaystyle S_\pm\) síkokat, a kettő közötti szakasz hosszának a kiszámításához alkalmazott közelítésünk (az ív helyettesítése egy egyenessel) nem megengedhető. Ennek legszembeötlőbb példája, amikor

\(\displaystyle m-\frac{d'}{2}<r<m+\frac{d'}{2}.\)

Ilyenkor a napfelkelte és a napnyugta összeér, nem megengedhető a \(\displaystyle d'\) elhanyagolása az \(\displaystyle m\) mellett, és a pontos ívhosszal kellene számolni. A számításaink során a \(\displaystyle \varphi\) változásával nem foglalkoztunk. Ez a változás a pólusokhoz nem túl közel egy napfelkelte alatt nagyságrendileg akkora pontatlanságot visz be az eredménybe, mint a ,,valódi nap'' (a Nap két delelése közti idő) és a forgás periódusa közötti különbség elhanyagolása. Végül megjegyezzük, a sarkok közvetlen közelében a napkelte és napnyugta időtartamát már jelentős részben befolyásolja a \(\displaystyle \psi\) változási üteme: azt, hogy a nap-éj egyenlőség idején egy ilyen pont mennyi ideig van a napkelte-napnyugta sávban, attól is függ, hogy maga a pólus mennyi idő alatt halad át ezen a sávon.

Mint azt fentebb már említettük, a Nap emelkedésének az \(\displaystyle \varepsilon\) szögét a horizont forgása határozza meg: a napfelkelte \(\displaystyle \Delta t\) időtartama alatt a Nap \(\displaystyle \Delta\eta\) szöget emelkedik, a horizont pedig \(\displaystyle \Delta t\omega\sin\varphi\) szöggel elfordul. Ebből következően

\(\displaystyle \varepsilon=\arctg\left(\frac{\Delta\eta}{\Delta t\omega\sin\varphi}\right)=\arctg\left(\frac{\sqrt{\cos^2\varphi-\sin^2\theta\cos^2\psi}}{\sin\varphi}\right)=\arctg\left(\frac{\sqrt{\cos^2\varphi-\sin^2\phi}}{\sin\varphi}\right)=\arccos\left(\frac{\sin\varphi}{\cos\phi}\right).\)

Néhány egyszerű térgeometriai megfontolás segítségével a napkelte helye (iránya) is meghatározható. Ehhez tekintsük a vizsgált ponthoz tartozó horizontális síkot!

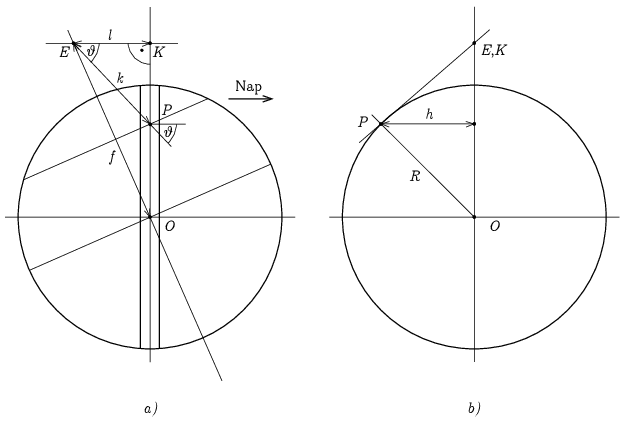
2. ábra

A 2/a ábrán (ami ugyanazt a nézetet mutatja, mint az 1/a ábra, ezért az ott szereplő mennyiségek itt nincsenek újra jelölve), \(\displaystyle P\) a vizsgált pont pozíciója akkor, amikor a napfelkelte éppen a felénél tart, és \(\displaystyle E\) az a pont, ahol a Föld forgástengelye a \(\displaystyle P\) horizontális síkját döfi. Mivel az \(\displaystyle OPE\sphericalangle\) szög derékszög, \(\displaystyle \overline{OE}=f=R/\sin\varphi\). Az \(\displaystyle E\) pontból a Nap felé irányuló egyenes benne fekszik a \(\displaystyle P\) horizontális síkjában, és a \(\displaystyle P\)-n átmenő, a Nap irányára merőleges síkot \(\displaystyle K\)-ban döfi. \(\displaystyle E\) és \(\displaystyle K\) az ábra síkjában van, de \(\displaystyle P\) \(\displaystyle h=\sqrt{r^2-m^2}\) távolságra kiemelkedik abból. A 2/b ábra a Nap felől nézve mutatja a helyzetet, ezen az \(\displaystyle E\) és \(\displaystyle K\) pontok fedésben vannak. Definíció szerint \(\displaystyle P\)-től \(\displaystyle E\) északra van, így az ábrán bejelölt (de nem az ábra síkjába illeszkedő) \(\displaystyle KEP\sphericalangle=\vartheta\) szög a napfelkelte pozícióját adja a déli iránytól mérve. Mivel

\(\displaystyle \overline{EP}=k=R\,\ctg\varphi\,,\qquad{\textrm{és}}\qquad\overline{EK}=l=f\cos\alpha=R\frac{\cos\psi\sin\theta}{\sin\varphi},\)

\(\displaystyle \vartheta=\arccos\left(\frac{l}{k}\right)=\arccos\left(\frac{\sin\theta\cos\psi}{\cos\varphi}\right)=\arccos\left(-\frac{\sin\phi}{\cos\varphi}\right).\)

II. megoldás. A Nap napi mozgása során 24 óra alatt tesz meg egy teljes kört a látszólagos pályáján, tehát 4 percenként egy fokot halad rajta. Ebből elhamarkodottan azt a téves következtetést vonhatnánk le, hogy a fél fokos emelkedéshez 2 percre van szükség. Azonban a napéjegyenlőségeket kivéve a látszólagos pálya nem egy főkör, (azaz a körpálya középpontja nem a Föld középpontja, hanem a tengely valamelyik pontja), így a Nap az égbolton (a napéjegyenlőségeket kivéve) ennél kisebb szögsebességgel mozog. Ezen kívül a Nap csak az Egyenlítőn kel fel és nyugszik le a horizontra merőlegesen (ott egész évben), máshol viszont (az évszaktól és a földrajzi helytől függően más-más) laposabb szögben. Mindkét hatás befolyásolja a napkelte és napnyugta időtartamát.

A Nap éves mozgása során látszólagosan az ekliptikán mozog a csillagokhoz képest, így az egyenlítő síkjához képesti szöge az év során folyamatosan változik \(\displaystyle \pm\phi_0\) szélsőértékek között, ahol \(\displaystyle \phi_0=23{,}4^\circ\), a Föld tengelyferdesége. Ha a Föld-pálya kicsiny excentricitásával nem foglalkozunk, akkor a szög változása első közelítésben

ahol \(\displaystyle \delta=\tfrac{d}{365,24\,\mathrm{nap}}2\pi\), és \(\displaystyle d\) a napok száma a nyári napfordulótól számítva (3. ábra).

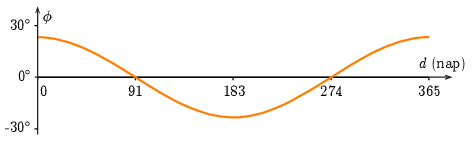
3. ábra

Megjegyzés. Ez a közelítés azt se veszi figyelembe, hogy a Nap az ekliptikán mozog (a körpálya közelítést használva) egyenletes sebességgel, de ezt levetítve az egyenlítőre már nem lesz egyenletes a mozgása. (Ez okozza az időegyenlet esetében is a féléves periódusú tagot, lásd a P. 3118. feladat megoldását a KöMaL 1999. áprilisi számában:
http://db.komal.hu/KomalHU/felhivatkoz.phtml?id=42077

Pontosabb eredményt kapunk a következőképpen: Vegyük fel a koordináta-rendszert úgy, hogy a \(\displaystyle z_0\) tengelye merőleges legyen az ekliptika síkjára, \(\displaystyle x_0\) tengelye pedig a tavaszpont felé (és így \(\displaystyle y_0\) tengelye a nyári napforduló irányába) mutasson. Ekkor a Földtől a Nap irányába mutató \(\displaystyle \boldsymbol{n_0}\) egységvektor, valamint a Föld tengelyének \(\displaystyle \boldsymbol{t}\) irányvektora:

A Nap irányvektora és az egyenlítő síkja által bezárt \(\displaystyle \phi\) szög a Nap irányvektora és a Föld tengelye által bezárt szög pótszöge, így

A két számítás között a napfordulókkor és a napéjegyenlőségekkor nincs eltérés, máskor legfeljebb \(\displaystyle 0{,}2^\circ\). A feladatunk megoldása szempontjából az (1) közelítés is elég (sőt már az is, hogy \(\displaystyle \phi=\phi_0\) a nyári napfordulókor, majd folyamatosan csökken, az őszi napéjegyenlőség idején \(\displaystyle \phi=0\), a téli napfordulókor \(\displaystyle \phi=-\phi_0\), és így tovább).

Ezután meghatározhatjuk, hogy a Nap adott \(\displaystyle \phi\) szög esetén (a deleléshez képest) mikor (és hol) kel fel, illetve nyugszik le. (Az időpont levezetése megtalálható az előbbi megjegyzésben említett P. 3118. feladat megoldásában is.)

Most vegyük fel a koordináta-rendszert úgy, hogy a \(\displaystyle z\) tengely a Föld forgástengelyével legyen párhuzamos, az \(\displaystyle y\) tengely pedig erre merőlegesen, a déli irányba mutasson (azaz a Nap az \(\displaystyle yz\) síkban legyen). Ekkor a Föld felszínének egy \(\displaystyle \varphi\) szélességű pontja felé mutató egységvektor:

\(\displaystyle \boldsymbol{r}=(-\cos\varphi\sin\tau,\,\cos\varphi\cos\tau,\,\sin\varphi),\)

ahol \(\displaystyle \tau=\tfrac{t}{24^\mathrm{h}}2\pi\) és \(\displaystyle t\) a deleléstől számított idő órákban, a Nap irányvektora pedig

Napkelte vagy napnyugta akkor van, amikor a Nap a horizonton látszik, azaz iránya merőleges az adott hely irányába (a zenit felé) mutató \(\displaystyle \boldsymbol{r}_\mathrm{h}=\boldsymbol{r}(\tau_\mathrm{h})\) egységvektorra:

Ez a kifejezés nem mindig ad megoldást \(\displaystyle \tau_\mathrm{h}\)-ra, hiszen (a sarkok közelében) lehet, hogy a Nap nem is kel fel, vagy le sem nyugszik az adott napon. Amennyiben van megoldása, akkor

\(\displaystyle t_{1,2}=\mp\tfrac{24^\mathrm{h}}{2\pi}\arccos(-\tg\varphi\tg\phi)\)

adja meg a Nap keltének, illetve nyugtának időpontját a deleléshez viszonyítva.

Megjegyzés. A napkelte és napnyugta tényleges időpontját a delelés időpontja határozza meg. Ez utóbbi egyrészt függ a választott időzónától és az adott hely és az időzóna középvonala közötti szögkülönbségtől, másrészt a fentebb említett P. 3118. feladatban is vizsgált időegyenlettől (amely körülbelül \(\displaystyle \pm15\) perc ingadozást okoz). Az időzónától való eltérés Budapesten (E19\(\displaystyle ^\circ\) és CET időzóna) \(\displaystyle +4^\circ\), ami 16 perc ,,sietést'' okoz, míg Helsinkiben (E25\(\displaystyle ^\circ\) és EET időzóna) \(\displaystyle -5^\circ\), ami 20 perc ,,késést'' eredményez. A két hatás miatt Budapesten a delelés időpontja a téli időszámítás idején \(\displaystyle 11^\mathrm{h}\,28'\) és \(\displaystyle 11^\mathrm{h}\,58'\) között, a nyári időszámítás idején pedig \(\displaystyle 12^\mathrm{h}\,28'\) és \(\displaystyle 12^\mathrm{h}\,50'\) között, míg Helsinkiben a téli időszámítás idején \(\displaystyle 12^\mathrm{h}\,03'\) és \(\displaystyle 12^\mathrm{h}\,34'\) között, a nyári időszámítás idején pedig \(\displaystyle 13^\mathrm{h}\,04\) és \(\displaystyle 13^\mathrm{h}\,24'\) között változik.

Bár a feladat nem kérdezi, érdemes meghatároznunk, hogy hol kel fel és hol nyugszik le a Nap, melyik égtáj irányába? Naivan azt gondolhatnánk, hogy a déli irányhoz képest \(\displaystyle \mp\tau_\mathrm{h}\) szögre, de ez nem így van! A \(\displaystyle \tau\) szöget a Nap (napi) pályája mentén, az egyenlítő síkjával párhuzamos körön mérjük, az égtájakat pedig a horizont síkjában. A két szögbeosztás (az időegyenlet levezetésénél láthatóval megegyezően most is) csak a \(\displaystyle 0^\circ\), \(\displaystyle \pm90^\circ\) és \(\displaystyle 180^\circ\) szögeknél egyezik meg.

A megfigyelő helye felé mutató egységvektor napkeltekor, illetve napnyugtakor

\(\displaystyle \boldsymbol{r}_\mathrm{h}=(\pm\cos\varphi\sin\tau_\mathrm{h},\,-\cos\varphi\cos\tau_\mathrm{h},\,\sin\varphi).\)

Napkeltekor, illetve napnyugtakor a horizonton a déli irányba mutató vektor erre merőleges, mégpedig úgy, hogy az \(\displaystyle \boldsymbol{r}_\mathrm{h}\) vektort a \(\displaystyle \tau_\mathrm{h}\) óraszögű síkban forgatjuk el déli irányba \(\displaystyle 90^\circ\)-kal:

\(\displaystyle \boldsymbol{d}_\mathrm{h}=(\pm\sin\varphi\sin\tau_\mathrm{h},\,-\sin\varphi\cos\tau_\mathrm{h},\,-\cos\varphi).\)

A felkelő vagy lenyugvó Nap \(\displaystyle \boldsymbol{n}\) irányvektora [(2)] ekkor szintén épp a horizont egy-egy pontjára mutat. A napkelte és napnyugta helyéhez éppen a \(\displaystyle \boldsymbol{d}_\mathrm{h}\) és \(\displaystyle \boldsymbol{n}\) vektorok által bezárt \(\displaystyle \vartheta\) szöget keressük. A szög koszinusza a skalárszorzat alapján, majd behelyettesítve (3)-at és rendezve:

Ha a (3) és (4) kifejezések alapján \(\displaystyle \vartheta\)-t és \(\displaystyle \tau_\mathrm{h}\)-t \(\displaystyle \phi\) (1)-es kifejezését felhasználva \(\displaystyle d\) függvényében ábrázoljuk (a 4. ábrán Budapesten), akkor láthatjuk, hogy \(\displaystyle \vartheta\) nagyobb amplitúdóval (Budapesten \(\displaystyle 36^\circ\), Helsinkiben \(\displaystyle 52{,}6^\circ\)) változik a keleti és nyugati irányt jelentő \(\displaystyle +90^\circ\) szög körül, mint \(\displaystyle \tau_\mathrm{h}\) (Budapesten \(\displaystyle 28{,}2^\circ\), Helsinkiben \(\displaystyle 48{,}5^\circ\), ami a napkelte, illetve napnyugta 1 óra 53 perces, illetve 3 óra 14 perces éves ingadozásnak felel meg a napéjegyenlőség idején tapasztalható deleléshez viszonyított 6 órás eltérés körül).

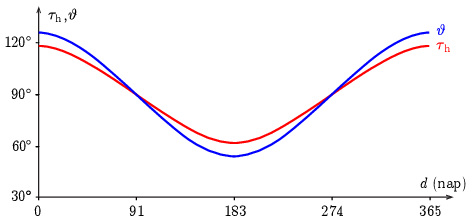
4. ábra

Ezután térjünk rá a feladatban megfogalmazott kérdésre: a napkelte (és napnyugta) időtartamára! A napkelte és napnyugta időpontjának meghatározásakor azt kerestük, hogy mikor merőleges a Föld középpontjától a megfigyelőhöz húzott vektor a Nap felé mutató vektorral: ekkor a két vektor skalárszorzatának nullát kellett adnia.

Ehhez hasonlóan, a két vektor skalárszorzatát felírva kiszámíthatjuk egy kicsiny \(\displaystyle \Delta t\) időponttal a napkelte után (vagy a napnyugta előtt) a Nap \(\displaystyle \Delta\eta\) magasságát a horizont felett. Mivel ez a szög a Nap zenittől mért távolságának pótszöge:

\(\displaystyle \sin\Delta\eta=\cos(90^\circ-\Delta\eta)=\boldsymbol{r}(\tau_\mathrm{h}-\Delta\tau)\boldsymbol{n},\)

ahol \(\displaystyle \Delta\tau=\tfrac{\Delta t}{24^\mathrm{h}}2\pi\). Behelyettesítve, a zárójeles kifejezést felbontva, felhasználva, hogy kis \(\displaystyle \Delta\eta\) és \(\displaystyle \Delta\tau\) szögekre \(\displaystyle \sin\Delta\eta\approx\Delta\eta\), \(\displaystyle \sin\Delta\tau\approx\Delta\tau\) és \(\displaystyle \cos\Delta\tau\approx 1\):

Ha \(\displaystyle \tau_\mathrm{h}\)-t (3)-ból kifejezzük és behelyettesítjük, majd a kifejezést tovább alakítjuk:

A napkelte és napnyugta \(\displaystyle \Delta t\) időtartamának meghatározása:

Látható, hogy az eredmény a földrajzi helytől (\(\displaystyle \varphi\)) és az évszaktól (\(\displaystyle \phi\)) függ. Az évszaktól való függés könnyebben látható, ha a (6) nevezőjében lévő kifejezést átalakítjuk:

\(\displaystyle \sqrt{\cos(\varphi+\phi)\cos(\varphi-\phi)}=\sqrt{\cos^2\phi-\sin^2\varphi}.\)

Rögzített \(\displaystyle \varphi\) esetén \(\displaystyle \phi=0\) esetén lesz a nevező maximális. Ez (talán meglepő módon) a tavaszi és az őszi napéjegyenlőségkor következik be, tehát ilyenkor lesz a napkelték és napnyugták időpontja mindenhol a legrövidebb:

\(\displaystyle \Delta t_\textrm{napéjegyenlőség}=\frac{2'}{\cos\varphi}.\)

Tehát a feladatunk kérdésére választ adva Helsinkiben (\(\displaystyle \varphi=60^\circ\)) a leggyorsabb napkelte (és napnyugta) időtartama a tavaszi és őszi napéjegyenlőség idején:

\(\displaystyle \Delta t_\mathrm{H, min}=\frac{2'}{\cos 60^\circ}=4'.\)

A leghosszabb időtartamokat mindenhol a nyári és téli napfordulókor figyelhetjük meg, amikor \(\displaystyle \phi=\pm\phi_0\) (3. ábra).

Áttérve a földrajzi helytől való függésre: az Egyenlítőnél \(\displaystyle \varphi=0^\circ\), így a (6) kifejezés

\(\displaystyle \Delta t_\mathrm{E}=\frac{2'}{\cos\phi}\)

alakra egyszerűsödik. \(\displaystyle -\phi_0\leq\phi\leq\phi_0\) alapján az időtartam \(\displaystyle 2'\) és \(\displaystyle 2'\,11''\) között lehet, az év során tehát alig változik.

Budapesten (\(\displaystyle \varphi=47{,}5^\circ\)) az időtartam hosszabb, és az év során már jelentősebben változik: \(\displaystyle 2'\,58''\) (tavaszi és őszi napéjegyenlőség) és \(\displaystyle 3'\,40''\) (nyári és téli napforduló) között.

Helsinkiben (\(\displaystyle \varphi=60^\circ\)) a minimális érték, ahogy láttuk \(\displaystyle 4'\), a maximális pedig \(\displaystyle 6'\,38''\) (,,kicsit több, mint hat és fél perc'', de nem csak karácsonykor, hanem Szent Iván napján is) (5. ábra).

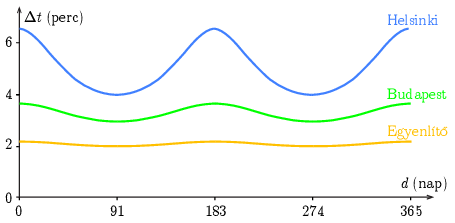
5. ábra

Tovább haladva észak felé, Luleåban (\(\displaystyle \varphi=65^\circ\,30'\)) már \(\displaystyle 4'\,49''\) és \(\displaystyle 16'\,45''\) között változik az időtartam (a sarkkörökhöz közeledve azonban a közelítéseink – a látszólagos pálya egyenes szakasszal való közelítése – egyre kevésbé jogosak). Láthatjuk, hogy \(\displaystyle \varphi\pm\phi>90^\circ\) (vagy \(\displaystyle \varphi\mp\phi<-90^\circ\)) esetén a (6) kifejezés nem ad eredményt: az északi sarkkörön túl nyáron egy ideig nem megy le, télen pedig nem kel fel a Nap (a déli sarkkörön túl pedig fordítva).

Végül – bár szintén nem része a feladatnak – vizsgáljuk meg a Nap pályájának meredekségét a horizontnál! Az (5) kifejezés megadja, hogy mekkora \(\displaystyle \Delta\eta\) szöggel emelkedik a Nap a horizont fölé, miközben a pályáján egy (kicsiny) \(\displaystyle \Delta\tau\) szöggel elfordul. Ahogy a bevezetőben említettük, a Nap napi mozgása során (általában) nem egy főkörön, hanem egy kisebb \(\displaystyle \cos\phi\) sugarú körön mozog, emiatt az égbolton az elmozdulása eközben csak \(\displaystyle \Delta\tau\cos\phi\) lesz. Ez alapján a Nap pályájának horizonttal bezárt \(\displaystyle \varepsilon\) szöge (érdemes áttérni a szög koszinuszára, mert az könnyebben értelmezhető eredményt ad):

Az Egyenlítőn (\(\displaystyle \varphi=0^\circ\)) a Nap pályája egész évben merőlegesen metszi a horizontot (\(\displaystyle \varepsilon=90^\circ\)). Minden más helyen a Nap a tavaszi és őszi napéjegyenlőség idején (amikor \(\displaystyle \phi=0^\circ\)) emelkedik a legmeredekebben, \(\displaystyle 90^\circ-\varphi\) szögben (Budapesten ez \(\displaystyle \varepsilon_\mathrm{max}=90^\circ-47{,}5^\circ=42{,}5^\circ\), Helsinkiben pedig \(\displaystyle \varepsilon_\mathrm{max}=90^\circ-60^\circ=30^\circ\)), míg a nyári és téli napforduló idején a leglaposabb (Budapesten \(\displaystyle \varepsilon_\mathrm{min}=36{,}5^\circ\)-os, Helsinkiben \(\displaystyle \varepsilon_\mathrm{min}=19{,}3^\circ\)-os) szögben (6. ábra).

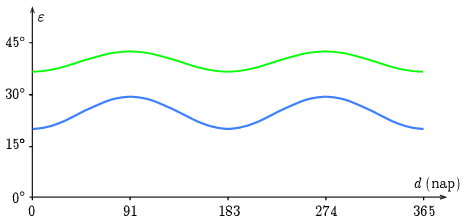
6. ábra

Megjegyzések. 1. A téli lapos emelkedést, amikor egész nap nem megy magasra a Nap, ,,ösztönösen'' érezni lehet, de a nyári eredmény először meglepő lehet, hiszen olyankor emelkedik a Nap a legmagasabbra. (A korábbi, a napkelte és napnyugta időtartamára kapott eredmény után persze már sejteni lehetett, hogy a meredekségnek nem nyáron, hanem tavasszal és ősszel van maximuma.) Szemléletesen mutatja a nyári lapos emelkedést, hogy például az északi sarkkörön a nyári napfordulókor a nap (északon) csak érinti a horizontot, tehát \(\displaystyle \varepsilon=0^\circ\).

2. A (3), (4) és (7) kifejezések összevetéséből láthatjuk, hogy

\(\displaystyle \cos\tau_\mathrm{h}=\cos\vartheta\cos\varepsilon,\)

amely igazolja, hogy a 2. ábrán megfigyelt \(\displaystyle \left|\vartheta-90^\circ\right|\geq\left|\tau_\mathrm{h}-90^\circ\right|\) egyenlőtlenség általánosságban is teljesül.

III. megoldás. Az II. megoldásban vektorokkal dolgoztunk. Most használjunk gömbi geometriát!

Bevezetés. A gömbi geometriában egy egységsugarú gömb felületén futó főkörök a síkgeometria egyeneseinek megfelelői. Egy főkör két pontját összekötő \(\displaystyle \pi\)-nél nem hosszabb ívet nevezzük gömbi szakasznak. Három, nem egy főkörön elhelyezkedő pont meghatároz egy gömbháromszöget: a pontokat összekötő szakaszok a gömb felületét két tartományra osztják, ezek közül a kisebb területű a gömbháromszög. A gömbháromszög \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) oldalai a csúcsokat összekötő gömbi szakaszok, melyek hossza a főkörívekhez tartozó középponti szögek. A gömbháromszög \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\) szögei a csúcsokban találkozó főkörök csúcsbeli érintő félegyenesei által bezárt szögek (amelyek megegyeznek a csúcsban találkozó főkörívekre fektetett síkok hajlásszögével).

A gömbháromszög oldalaira és szögeire a síkbeli háromszöghöz hasonlóan összefüggések írhatók fel. Ezek közül használni fogjuk a gömbi szinusztételt:

\(\displaystyle \frac{\sin\alpha}{\sin\beta}=\frac{\sin a}{\sin b},\)

az oldalakra vonatkozó gömbi koszinusztételt:

\(\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos\gamma,\)

valamint a gömbi Pitagorasz-tételt (amely az utóbbi speciális esete, ha \(\displaystyle \gamma=90^\circ\)):

\(\displaystyle \cos c=\cos a\cos b.\)

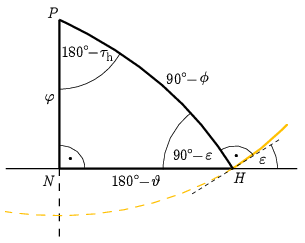
7. ábra

A 7. ábrán egy olyan gömbháromszöget rajzoltunk fel, amelyet egy a \(\displaystyle \varphi\) szélességi körön lévő helyről látunk észak felé nézve. A háromszög \(\displaystyle P\) csúcsa a Sarkcsillag (Polaris), \(\displaystyle N\) csúcsa a horizont északi pontja, \(\displaystyle H\) csúcsa pedig a horizontnak az a pontja, ahol a Nap felkel. A gömbháromszög oldalai az (egységsugarú) gömb főkörívei, hosszukat a hozzájuk tartozó középponti szögek adják meg. Eszerint

A gömbháromszög szögei:

A \(\displaystyle H\) ponton átmenő görbe (általában nem főkör) a nap pályája, amelynek \(\displaystyle H\)-beli érintője merőleges a \(\displaystyle \overline{PH}\) gömbi szakaszra (hiszen napi mozgása során a Nap a Sarkcsillag körüli körpályán mozog).

Az előkészületek után már nagyon gyorsan megkapjuk a II. megoldásban is levezetett összefüggéseket.

1. Írjuk fel a gömbi szinusz-tételt:

\(\displaystyle \frac{\sin(90^\circ-\varepsilon)}{\sin 90^\circ}=\frac{\sin\varphi}{\sin(90^\circ-\phi)},\)

amiből a felkelő (és lenyugvó) Nap pályájának horizonttal bezárt szögére a

\(\displaystyle \cos\varepsilon=\frac{\sin\varphi}{\cos\phi}\)

összefüggés adódik, a (7) kifejezéssel összhangban.

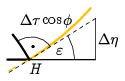
8. ábra

Miközben a Nap \(\displaystyle \Delta\eta=0{,}5^\circ\) szöget emelkedik, a \(\displaystyle 2\pi\cos\phi\) kerületű pályáján \(\displaystyle \Delta\tau\cos\phi\) szöget halad. Így a 8. ábrán látható kicsiny síkháromszögre:

\(\displaystyle \sin\varepsilon=\frac{\Delta\eta}{\Delta\tau\cos\phi},\)

amelyből (\(\displaystyle \cos\varepsilon\) előbbi kifejezését is felhasználva) már megkapható a napkelte (és napnyugta) feladatban kérdezett \(\displaystyle \Delta t\) időtartama:

a (6) kifejezéssel megegyezően.

2. A gömbi Pitagorasz-tételt szerint:

\(\displaystyle \cos(90^\circ-\phi)=\cos\varphi\cos(180^\circ-\vartheta),\)

amiből azonnal

\(\displaystyle \cos\vartheta=-\frac{\sin\phi}{\cos\varphi}\)

adódik, a (4) összefüggéssel összhangban.

3. Az oldalakra vonatkozó gömbi koszinusztétel alapján:

\(\displaystyle \cos(180^\circ-\vartheta)=\cos\varphi\cos(90^\circ-\phi)+\sin\varphi\sin(90^\circ-\phi)\cos(180^\circ-\tau_\mathrm{h}),\)

amiből az előbbi eredményt is felhasználva

\(\displaystyle \cos\tau_\mathrm{h}=\frac{\cos\vartheta+\cos\varphi\sin\phi}{\sin\varphi\cos\phi}=\frac{-\frac{\sin\phi}{\cos\varphi}+\cos\varphi\sin\phi}{\sin\varphi\cos\phi}=-\tg\varphi\tg\phi,\)

a (3) kifejezéssel megegyezően.

Statisztika:

7 dolgozat érkezett.
6 pontot kapott:	Dobos Anita, Erős Fanni, Fehérvári Donát.
5 pontot kapott:	Hegedüs Márk.
4 pontot kapott:	2 versenyző.
3 pontot kapott:	1 versenyző.

A KöMaL 2024. májusi fizika feladatai