 |
A P. 5580. feladat (2024. szeptember) |
P. 5580. Két testvér a lakásuk lépcsőházában (vízszintesen mérve) \(\displaystyle 4{,}5~\mathrm{m}\) távolságból ,,zoknicsatázik'' az ábra szerint. Anikó a pihenőről, \(\displaystyle 4~\mathrm{m}\) magasságból \(\displaystyle 6~\mathrm{m/s}\), Bálint pedig \(\displaystyle 1{,}5~\mathrm{m}\) magasságból, a vízszintessel \(\displaystyle 45^\circ\)-os szöget bezáró \(\displaystyle 8~\mathrm{m/s}\) kezdősebességgel dobja el a zoknigombócot. Határozzuk meg a két gombóc legkisebb távolságát, ha a gyerekek egyszerre dobták el azokat! (A közegellenállást ne vegyük figyelembe.)
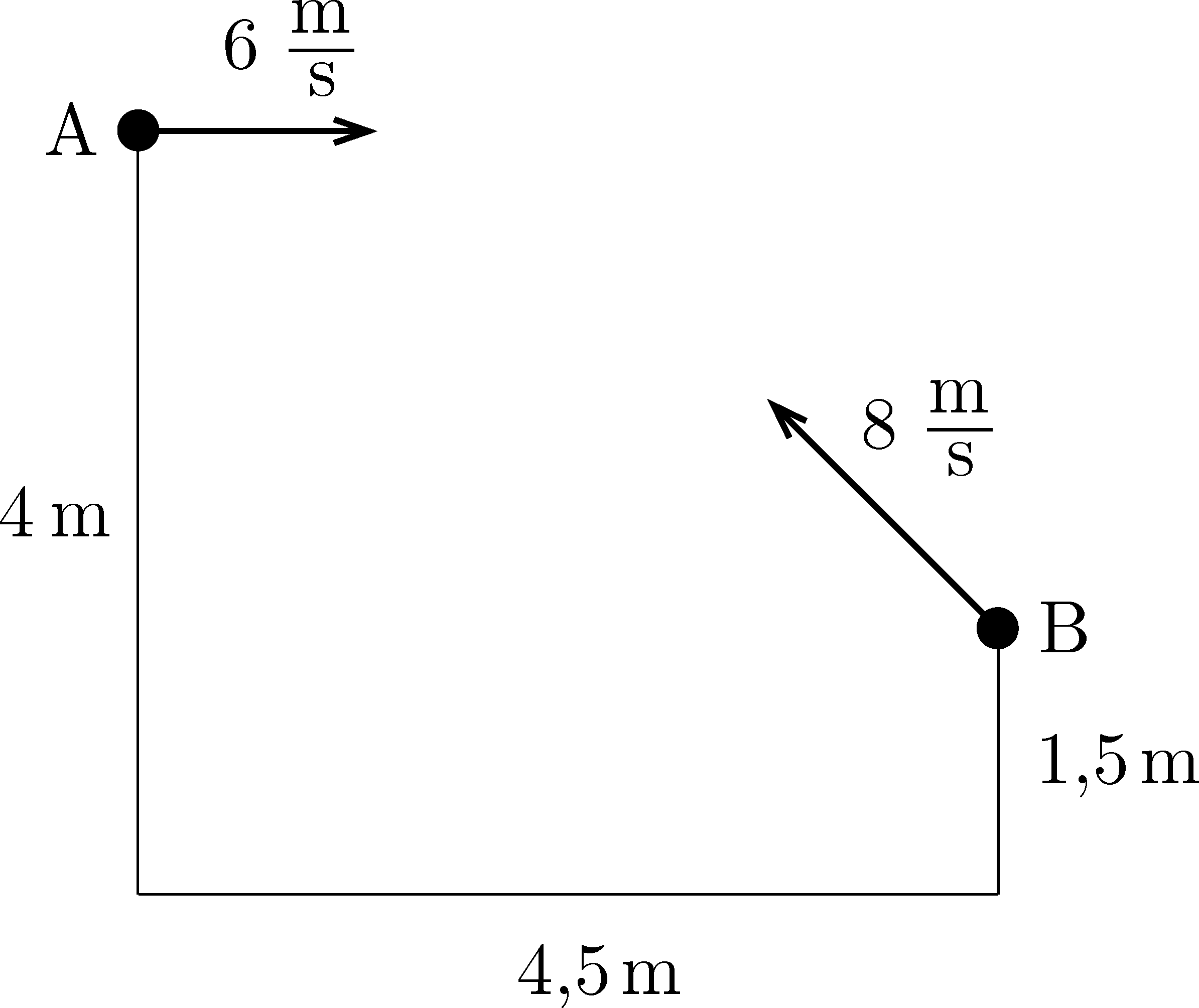
Közli: Kis Tamás, Heves
(4 pont)
A beküldési határidő 2024. október 15-én LEJÁRT.
Megoldás. Vizsgáljuk a két test mozgását az \(\displaystyle A\) pontból eldobott testtel együtt mozgó (vízszintesen \(\displaystyle v_A=6\,\mathrm{m/s}\) sebességgel egyenletesen mozgó, függőlegesen lefelé \(\displaystyle g\) gyorsulással gyorsuló) koordináta-rendszerből. Ebben a rendszerben a \(\displaystyle B\) pontból \(\displaystyle v_B=8\,\mathrm{m/s}\) sebességgel eldobott test \(\displaystyle \boldsymbol{v}_\mathrm{rel}=\boldsymbol{v}_B-\boldsymbol{v}_A\) sebességgel egyenes vonalú egyenletes mozgást végez, sebességének iránya a vízszintessel
\(\displaystyle \alpha=\arctg\frac{v_B\sin 45^\circ}{v_A+v_B\cos 45^\circ}=\arctg\frac{4\sqrt{2}}{6+4\sqrt{2}}=25{,}9^\circ\)
szöget zár be. (Az \(\displaystyle A\) pont pedig értelemszerűen nyugalomban van.)
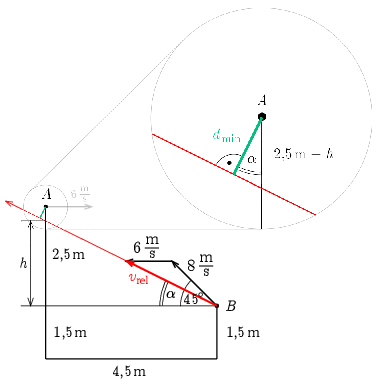
Az ábra alapján \(\displaystyle h=4{,}5\,\mathrm{m}\cdot\tg\alpha=2{,}18\,\mathrm{m}\), a két eldobott test közötti minimális távolság pedig a kinagyított ábrarészlet alapján \(\displaystyle d_\mathrm{min}=(2{,}5\,\mathrm{m}-h)\cos\alpha=0{,}28\,\mathrm{m}=28\,\mathrm{cm}\).
Statisztika:
75 dolgozat érkezett. 4 pontot kapott: Agócs Zoltán, Bálint Áron, Beke Márton Csaba, Bélteki Teó, Bencze Mátyás, Bense Tamás, Blaskovics Ádám, Bús László Teodor, Csapó András, Csiszár András, Domján Noémi Dóra, Éliás Kristóf , Erdélyi Dominik, Erős Fanni, Fekete Lúcia, Földi Albert, Gyenes Károly, Hajós Boróka, Hornok Máté, Horvath Benedek, Kiss 131 Adorján Timon, Klement Tamás, Kovács Dániel, Kovács Tamás, Magyar Zsófia, Masa Barnabás, Misik Balázs, Molnár Lili, Papp Emese Petra, Simon János Dániel, Szabó Márton, Tóth Hanga Katalin, Tóth-Tűri Bence, Ujvári Sarolta, Varga 511 Vivien, Vértesi Janka, Vincze Anna, Zólomy Csanád Zsolt. 3 pontot kapott: Beinschroth Máté, Kis Boglárka 08, Nagy Gellért Ákos, Orbán Jázmin, Sütő Áron, Szécsi Bence, Zádori Gellért, Zámbó Luca. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 11 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2024. szeptemberi fizika feladatai
