 |
A P. 5581. feladat (2024. szeptember) |
P. 5581. Vékony, rugalmas acélszalagból két különböző sugarú karikát készítünk. A vízszintes asztalon csúszó karikákra (viszkózus jellegű) fékezőerő hat, ami arányos a karikák sugarával és a pillanatnyi sebességükkel. Ha a kisebbik karikát v0 sebességgel meglökjük, akkor a teljes megállásig L0 utat tesz meg. Lökjük meg az egyik karikát úgy, hogy nekiütközzön a kezdetben álló másiknak, és az ütközés előtt a sebessége v legyen. Egymástól milyen távolságra állnak meg a karikák, ha az ütközés rugalmas és
a) egyenes,
b) tetszőleges?
A karikák sem az ütközés előtt, sem utána nem forognak, méretük az ütközés után megtett utakhoz képest elhanyagolható.
Példatári feladat nyomán
(5 pont)
A beküldési határidő 2024. október 15-én LEJÁRT.
Megoldás. Egyenes ütközés esetén a karikák középpontja egy egyenes mentén mozog, emiatt az elmozdulás, sebesség és gyorsulás (előjeles) skalár mennyiségekkel adható meg. Nem egyenes ütközésnél az elmozdulás, a sebesség és a gyorsulás (síkbeli) vektorokkal írható le. Ez utóbbi az általánosabb eset, ami magában foglalja az egyenes ütközést is.
A karikák tömege arányos a méretükkel (sugarukkal), emiatt a fékezőerő így írható fel: \displaystyle \boldsymbol{F}=-km\boldsymbol{v}, ahol \displaystyle k egy állandó. A Newton-féle mozgásegyenlet szerint
\displaystyle m\boldsymbol{a}=-km\boldsymbol{v},
vagyis
\displaystyle \boldsymbol{a}+k\boldsymbol{v}=0.
Mivel a gyorsulásvektor a sebességvektor időbeli változásának ütemével (idő szerinti deriváltjával) egyezik meg, a sebességvektor pedig az \displaystyle \boldsymbol{r} helyvektor változási ütemét adja meg, ha \displaystyle \boldsymbol{a}+k\boldsymbol{v}=0, akkor
| \displaystyle (1) | \displaystyle \boldsymbol{v}+k\boldsymbol{r}=\text{állandó vektor}, |
hiszen a változásának üteme nulla. Ha valamelyik karika kezdetben az \displaystyle \boldsymbol{r}_0 helyen \displaystyle \boldsymbol{v}_0 sebességgel mozgott, és az \displaystyle r_1 helyen áll meg, akkor az (1) megmaradási tétel szerint
\displaystyle \boldsymbol{v}_0+k\boldsymbol{r}_0=k\boldsymbol{r}_1,
vagyis az elmozdulásvektor az indulástól a megállásig:
\displaystyle \boldsymbol{L}_0=\boldsymbol{r}_1-\boldsymbol{r}_0=\frac{1}{k}\,\boldsymbol{v}_0.
A megadott feltétel szerint \displaystyle L_0=v_0/k, vagyis \displaystyle k=v_0/L_0. Ennek megfelelően a karika elmozdulásvektora a \displaystyle \boldsymbol{v} kezdősebességű indulástól a megállásig
\displaystyle \boldsymbol{L}=\frac{L_0}{v_0}\boldsymbol{v}.
Megjegyzés. A karika
\displaystyle \frac{\mathrm{d}v(t)}{\mathrm{d}t}=-kv(t)
mozgásegyenlete a radioaktív bomlások egyenletével azonos alakú, és a megoldása:
\displaystyle v(t)=v_0\mathrm{e}^{-kt}.
Látszik, hogy véges hosszúságú idő alatt a sebesség nem válik nullává, tehát a karika elvben sohasem áll meg. Másrészt igaz, hogy néhányszor (mondjuk 5-ször) \displaystyle 1/k idő alatt a sebesség a kezdeti értéknek olyan kicsiny részére csökken, hogy gyakorlatilag nullának tekinthető.
a) Legyen a kezdetben álló karika tömege \displaystyle M, a nekiütköző karikáé \displaystyle m. Az ütközés utáni sebességeket jelölje \displaystyle \boldsymbol{U} és \displaystyle \boldsymbol{u} (1. ábra).
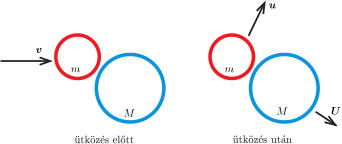
1. ábra
Egyenes ütközés esetén a sebességvektorok helyett elegendő azok (előjeles) nagyságával, \displaystyle U-val és \displaystyle u-val számolni. Nyilván \displaystyle U>u, és a két karika távolsága a megállásukkor
\displaystyle L=\frac{L_0}{v_0}U-\frac{L_0}{v_0}u=\frac{L_0}{v_0}(U-u).
Az impulzus- és az energiamegmaradás törvénye szerint
\displaystyle mv=mu+MU,\qquad\text{illetve}\qquad\frac{1}{2}mv^2=\frac{1}{2}mu^2+\frac{1}{2}MU^2.
Ez a két összefüggés egyértelműen meghatározza az ütközés utáni sebességeket:
\displaystyle u=\frac{m-M}{m+M}v,\qquad U=\frac{2m}{m+M}v,
tehát
\displaystyle U-u=\frac{2m}{m+M}v-\frac{m-M}{m+M}v=v,
és a keresett távolság:
\displaystyle L=\frac{v}{v_0}L_0.
Érdekes, hogy ez a távolság a karikák méretétől (tömegétől) függetlenül minden esetben ugyanakkora.
b) Ha az ütközés nem egyenes, a megmaradási törvények nem határozzák meg egyértelműen a karikák ütközés utáni sebességét. Ennek ellenére igaz, hogy
\displaystyle \vert\boldsymbol{U}-\boldsymbol{u}\vert=v,
és emiatt a karikák elmozdulásvektorai \displaystyle \boldsymbol{R}=\frac{L_0}{v_0}\boldsymbol{U} és \displaystyle \boldsymbol{r}=\frac{L_0}{v_0}\boldsymbol{u}, a végső távolságuk pedig
\displaystyle L=\vert\boldsymbol{R}-\boldsymbol{r}\vert=\vert\boldsymbol{U}-\boldsymbol{u}\vert\,\frac{L_0}{v_0}=\frac{v}{v_0}L_0.
Az ütközés utáni relatív sebesség nagyságáról háromféle módszerrel is belátjuk, hogy az \displaystyle v-vel egyezik meg.
1. módszer: Megmaradási törvények alkalmazása. Az impulzus- és az energiamegmaradás törvénye szerint
\displaystyle m\boldsymbol{v}=m\boldsymbol{u}+M\boldsymbol{U},\qquad\text{illetve}\qquad\frac{1}{2}mv^2=\frac{1}{2}mu^2+\frac{1}{2}MU^2,
vagyis
| \displaystyle (2) | \displaystyle \boldsymbol{v}=\boldsymbol{u}+\frac{M}{m}\boldsymbol{U}, |
és
| \displaystyle (3) | \displaystyle v^2=u^2+\frac{M}{m}U^2. |
A (2) egyenlet négyzetét (önmagával való skaláris szorzatát) (3)-mal összevetve kapjuk, hogy
| \displaystyle (4) | \displaystyle 2\boldsymbol{u}\cdot\boldsymbol{U}=\left(1-\frac{M}{m}\right)\,U^2. |
Számítsuk ki most az \displaystyle \boldsymbol{U}-\boldsymbol{u} vektor önmagával való skalárszorzatát, vagyis a relatív sebesség négyzetét:
\displaystyle \left(\boldsymbol{U}-\boldsymbol{u}\right)^2=U^2+u^2-2\boldsymbol{u}\cdot\boldsymbol{U}.
Felhasználva a (4), majd a (3) összefüggést, megkapjuk, hogy
\displaystyle \left(\boldsymbol{U}-\boldsymbol{u}\right)^2=U^2+u^2-\left(1-\frac{M}{m}\right)\,U^2=u^2+\frac{M}{m}U^2=v^2,
tehát \displaystyle \vert\boldsymbol{U}-\boldsymbol{u}\vert=v.
2. módszer: Tömegközépponti rendszer előnyei. Ha két test relatív sebessége valamely vonatkoztatási rendszerben \displaystyle \Delta\boldsymbol{v}, akkor bármely másik, az eredetihez képest mozgó koordináta-rendszerben az egymáshoz viszonyított sebesség ugyanekkora \displaystyle \Delta\boldsymbol{v}. A ,,mozgó'' rendszerre való áttéréskor mindegyik sebességhez ugyanaz a vektor (a vonatkoztatási rendszerek egymáshoz viszonyított sebessége) adódik hozzá, ez tehát a sebességvektorok különbségéből kiesik. (Fizikus szaknyelven szólva: a relatív sebesség Galilei-invariáns mennyiség.)
Két test tömegközépponti (TKP) rendszerében a testek impulzusa (lendülete) \displaystyle \boldsymbol{p} és \displaystyle -\boldsymbol{p}. A testek rugalmas ütközésekor az impulzusok a TKP-i rendszerben \displaystyle \boldsymbol{p}' és \displaystyle -\boldsymbol{p}'-re változnak. Amennyiben az ütközés rugalmas, a \displaystyle p^2-tel, illetve \displaystyle p'^2-tel arányos mozgási energia megmaradó mennyiség, fennáll tehát \displaystyle \vert\boldsymbol{p}\vert=\vert\boldsymbol{p}'\vert. A testek sebessége a TKP-i rendszerben egymással ellentétes irányú. A sebességkülönbség is arányos \displaystyle p-vel, illetve \displaystyle p'-vel. Mivel az ütközésnél az impulzusok nagysága nem változik, a sebességkülönbségek nagysága is változatlan marad (2. ábra).
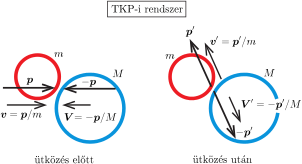
2. ábra
Az eredeti (laboratóriumi) rendszerben a sebességkülönbség nagysága \displaystyle v. A Galilei-invariancia miatt ugyanekkora kell, hogy legyen az ütközés utáni sebességkülönbség is, vagyis \displaystyle \vert\boldsymbol{U}-\boldsymbol{u}\vert=v.
3. módszer: Síkbeli vektorok komplex számokkal. A KöMaL 2024. évi áprilisi számában megjelent Komplex számok a fizikában I. cikk szerint bármely síkbeli \displaystyle \boldsymbol{w}=(w_x,w_y) vektornak kölcsönösen egyértelműen megfeleltethető egy komplex szám: \displaystyle w^*=w_x+iw_y. (A \displaystyle ^* azt jelzi, hogy komplex számról van szó, amely különbözik a \displaystyle \boldsymbol{w} vektor \displaystyle w-vel jelölt hosszától.)
A ,,komplex vektorokkal'' kényelmesen tárgyalhatók bizonyos fizikai problémák, pl. síkban mozgó testek ütközése. Az idézett cikkben leírtak szerint (a jelöléseket a jelen esethez igazítva), ha egy \displaystyle M tömegű, álló karikának egy másik, \displaystyle m tömegű karika \displaystyle w^*=v sebességgel nekiütközik, akkor a két test sebessége az ütközés után
\displaystyle u^*=\left(\frac{m}{M+m}+\frac{M}{M+m}\mathrm{e}^{2i\alpha}\right)v\qquad\text{és}\qquad U^*=\frac{m}{M+m}\left(1-\mathrm{e}^{2i\alpha}\right)v,
ahol \displaystyle \alpha az ütközés ,,ferdeségére'' jellemző szög. A két test relatív sebessége
\displaystyle u^*-U^*=\mathrm{e}^{2i\alpha}\,v,
melynek nagysága (a komplex szám abszolút értéke):
\displaystyle \vert\boldsymbol{u}-\boldsymbol{U}\vert=\vert u^*-U^*\vert=\left|\mathrm{e}^{2i\alpha}\right|v=v.
Statisztika:
18 dolgozat érkezett. 5 pontot kapott: Beke Márton Csaba, Simon János Dániel, Tóth Kolos Barnabás, Ujpál Bálint, Ujvári Sarolta, Zólomy Csanád Zsolt. 4 pontot kapott: Gyenes Károly, Kiss 131 Adorján Timon, Kovács Tamás, Sütő Áron. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2024. szeptemberi fizika feladatai
|
|

