 |
A P. 5582. feladat (2024. szeptember) |
P. 5582. A Cassini-űrszonda adatainak feldolgozásával látványos videó (https://www.flickr.com/photos/kevinmgill/44583965185/) készült, amelyen az látható, hogy a Jupiter Europa holdja ,,lehagyja'' az Io nevű holdat. Ez látszólag ellentmond a Kepler-törvényeknek, hiszen a Jupiterhez közelebb lévő Io keringési sebessége nagyobb, mint a távolabbi Europa holdé. A paradoxon feloldása: a Cassini-szonda is mozgott, amikor a felvétel készült. Legfeljebb milyen messze lehet a Jupitertől egy, a bolygó körül keringő űrszonda, és milyen irányba kering, hogy egy ilyen furcsa ,,szerepcsere'' létrejöjjön? Tekintsük úgy, hogy a holdak és az űrszonda közel azonos síkban, körpályákon keringenek.
Közli: Gnädig Péter, Vácduka
(5 pont)
A beküldési határidő 2024. október 15-én LEJÁRT.
Megoldás. Belátjuk, hogy a leírt jelenség csak akkor jöhet létre, ha az űrszonda a holdakkal ellentétes irányba kering a Jupiter körül.
Megjegyzés. A Cassini űrszonda ténylegesen nem keringett a Jupiter körül, hanem elhaladt az óriásbolygó mellett, és annak gravitációs lendítését (is) kihasználva jutott el a Szaturnusz közelébe. Emiatt szerepel a feladat szövegében ,,egy, a bolygó körül keringő űrszonda'', ami tehát nem a Cassini.
Jelöljük az Io keringési sugarát (a Jupiter középpontjától mért átlagos távolságot) \(\displaystyle r_1\)-gyel, az Europa pályasugarát \(\displaystyle r_2\)-vel, az űrszondáét pedig \(\displaystyle R\)-rel. A megfelelő keringési sebességek legyenek \(\displaystyle v_1,\,v_2\) és \(\displaystyle V\).
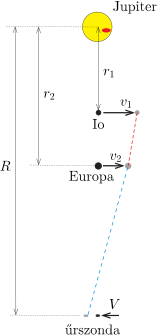
Az ábráról leolvasható, hogy a 2-es jelzésű Europa akkor tudja – látszólag – megelőzni az 1-es jelzésű Io holdat, ha egy kicsiny \(\displaystyle t\) idő alatt teljesül, hogy
| \(\displaystyle (1)\) | \(\displaystyle \frac{v_2t+Vt}{R-r_2} >\frac{v_1t+Vt}{R-r_1}.\) |
Használjuk még ki, hogy Kepler III. törvénye szerint
\(\displaystyle T^2\sim \frac{r^2}{v^2}\sim r^3,\qquad \text{vagyis}\qquad v \sim \frac{1}{\sqrt{r}}.\)
Eszerint (1) így is felírható:
\(\displaystyle \frac{\frac{1}{\sqrt{r_2}}+\frac{1}{\sqrt{R}}}{R-r_2}>\frac{\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{R}}}{R-r_1},\)
azaz
\(\displaystyle \frac{1}{\sqrt{Rr_2}\left(\sqrt{R}-\sqrt{r_2}\right)}>\frac{1}{\sqrt{Rr_1}\left(\sqrt{R}-\sqrt{r_1}\right)},\)
tehát
\(\displaystyle \sqrt{r_1}\left(\sqrt{R}-\sqrt{r_1}\right)>\sqrt{r_2}\left(\sqrt{R}-\sqrt{r_2}\right),\)
| \(\displaystyle (2)\) | \(\displaystyle \sqrt{R} \left(\sqrt{r_2}-\sqrt{r_1}\right)<r_2-r_1,\) |
és így
\(\displaystyle \sqrt{R}<\frac{r_2-r_1}{\sqrt{r_2}-\sqrt{r_1}}=\sqrt{r_1}+\sqrt{r_2},\)
azaz
| \(\displaystyle (3)\) | \(\displaystyle R<\Bigl(\sqrt{r_1}+\sqrt{r_2}\Bigr)^2.\) |
Megjegyzés. Ha az űrszonda a holdakkal megegyező irányba kering, akkor (1)-ben \(\displaystyle V\) előjele negatívra változik, és a fentiekkel megegyező lépések után (2) helyett a
| \(\displaystyle (2^*)\) | \(\displaystyle \sqrt{R} \left(\sqrt{r_1}-\sqrt{r_2}\right)>r_2-r_1 \) |
feltételt kapjuk. Ez azonban semekkora \(\displaystyle R\)-re nem teljesül, hiszen \(\displaystyle r_1<r_2\) miatt a bal oldal negatív, a jobb oldal pedig pozitív.
Táblázati adatok szerint \(\displaystyle r_1=421{,}8\cdot 10^3\,\mathrm{km}\) és \(\displaystyle r_2=671{,}8\cdot 10^3\,\mathrm{km}\), innen (3)-ból kapjuk: az űrszonda pályasugara legfeljebb 2,16 millió km lehet.
Statisztika:
16 dolgozat érkezett. 5 pontot kapott: Bélteki Teó, Kovács Tamás, Tóthpál-Demeter Márk, Ujpál Bálint, Zólomy Csanád Zsolt. 4 pontot kapott: Horvath Benedek. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 2 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2024. szeptemberi fizika feladatai