A P. 5583. feladat (2024. szeptember)

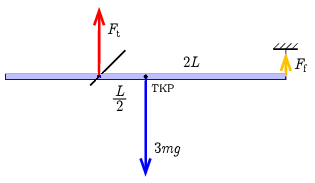
P. 5583. Az ábrán látható $\displaystyle 3m$ tömegű és $\displaystyle 3L$ hosszúságú vékony, homogén tömegeloszlású rúd az egyik végétől $\displaystyle L$ távolságra lévő vízszintes tengely körül függőleges síkban súrlódásmentesen foroghat. A rudat a másik végéhez csatlakozó függőleges fonál segítségével vízszintesen tartjuk.

$\displaystyle a)$ Mekkora erőt fejt ki a fonál és a tengely a rúdra ebben az egyensúlyi állapotban?

$\displaystyle b)$ A fonál elvágását követően mekkora lesz a rúd alsó végpontjának sebessége akkor, amikor a rúd a függőleges egyenesen halad át?

$\displaystyle c)$ Mekkora ebben a pillanatban a tengely által kifejtett erő?

Közli: Veres Dénes, Szolnok

(4 pont)

A beküldési határidő 2024. október 15-én LEJÁRT.

Megoldás. a) Az erőegyensúly és forgatónyomaték-egyensúly (a tengelyre vonatkoztatva):

amiből a tengely és a fonál által kifejtett (függőlegesen felfelé mutató) erő

$\displaystyle F_\mathrm{t}=\frac{9}{4}mg,\qquad\textrm{illetve}\qquad F_\mathrm{f}=\frac{3}{4}mg.$

b) A mechanikai energia megmaradása alapján

$\displaystyle 3mg\frac{L}{2}=\frac{1}{2}\Theta\omega^2,$

ahol

$\displaystyle \Theta=\Theta_0+3m\left(\frac{L}{2}\right)^2=\frac{1}{12}\cdot 3m\left(3L\right)^2+3m\left(\frac{L}{2}\right)^2=3mL^2.$

Ebből a rúd szögsebessége

$\displaystyle \omega=\sqrt{\frac{g}{L}},$

a végpont sebessége pedig

$\displaystyle v=2L\omega=2\sqrt{Lg}.$

c) A legalsó helyzetben a függőleges erők eredője gyorsítja a tömegközéppontot a tengely felé:

$\displaystyle F_\mathrm{t}'-3mg=3m\omega^2\frac{L}{2},$

amiből a tengely által (függőlegesen felfelé) kifejtett erő:

$\displaystyle F_\mathrm{t}'=3m\omega^2\frac{L}{2}+3mg=\frac{9}{2}mg.$

Statisztika:

79 dolgozat érkezett.
4 pontot kapott:	Agócs Zoltán, Beke Márton Csaba, Bélteki Teó, Bús László Teodor, Csiszár András, Fekete Lúcia, Horvath Benedek, Kis Boglárka 08, Kovács Tamás, Misik Balázs, Monok Péter, Rózsa Laura Enikő , Szabó Márton, Szécsi Bence, Ujpál Bálint, Varga 511 Vivien, Vincze Anna.
3 pontot kapott:	Domján Noémi Dóra, Éliás Kristóf , Erdélyi Dominik, Gyenes Károly, Hasulyó Dorián, Kiss 131 Adorján Timon, Klement Tamás, Magyar Zsófia, Nagy Gellért Ákos, Papp Emese Petra, Simon János Dániel, Tóth Hanga Katalin.
2 pontot kapott:	28 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2024. szeptemberi fizika feladatai