 |
A P. 5584. feladat (2024. szeptember) |
P. 5584. Egy szappanos vízbe mártott keret hártyájára zárt cérnahurkot teszünk, majd a hurok közepét egy tűvel kilyukasztjuk. A cérnahurok körré feszül. Adjuk meg a körben a feszítőerő nagyságát a sugár és a felületi feszültség függvényében!
Közli: Gelencsér Jenő, Kaposvár
(4 pont)
A beküldési határidő 2024. október 15-én LEJÁRT.
Megoldás. Jelöljük a szappanos víz felületi feszültségét α-val. Ekkor a szappanhártya egységnyi hosszúságú darabjára annak határán (a hártya 2 oldalát is figyelembe véve) 2α nagyságú, a határgörbe érintőjére merőleges erő hat.
Tekintsük a cérnahurok gondolatban kettévágott, a 2r hosszúságú vágás mentén egy merev pálcikával lezárt részét. Az elvágott fonál két végén ható, összesen 2F nagyságú erő tart egyensúlyt a hártyának a félkör mentén kifejtett húzóerejével (lásd az ábra bal oldali felét).
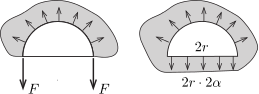
Ha a kör átmérője mentén elhelyezkedő, 2r hosszúságú pálca másik oldalán is szappanhártya feszülne, az összesen 2r⋅2α erőt fejtene ki, és a zárt félkör a határán ható (a felületi feszültségből származó) erők hatására egyensúlyban maradna (lásd az ábra jobb oldali felét).
A két elrendezést összevetve mondhatjuk, hogy
2F=2r⋅2α,
vagyis a fonalat feszítő erő
F=2rα.
Statisztika:
27 dolgozat érkezett. 4 pontot kapott: Agócs Zoltán, Bélteki Teó, Horvath Benedek, Klement Tamás, Masa Barnabás, Papp András, Ujpál Bálint. 3 pontot kapott: Csiszár András, Zádori Gellért. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2024. szeptemberi fizika feladatai
|
|

