 |
A P. 5586. feladat (2024. szeptember) |
P. 5586. Egy négyzet keresztmetszetű üvegrudat az ábrán látható alakban meghajlítunk. Az \(\displaystyle A\) felületre merőlegesen beeső, párhuzamos fénynyaláb érkezik. Legalább mekkora az \(\displaystyle R/d\) arány, ha az \(\displaystyle A\) felületre eső fény teljes egészében a \(\displaystyle B\) felületen hagyja el az \(\displaystyle n=1{,}5\) törésmutatójú üvegrudat?
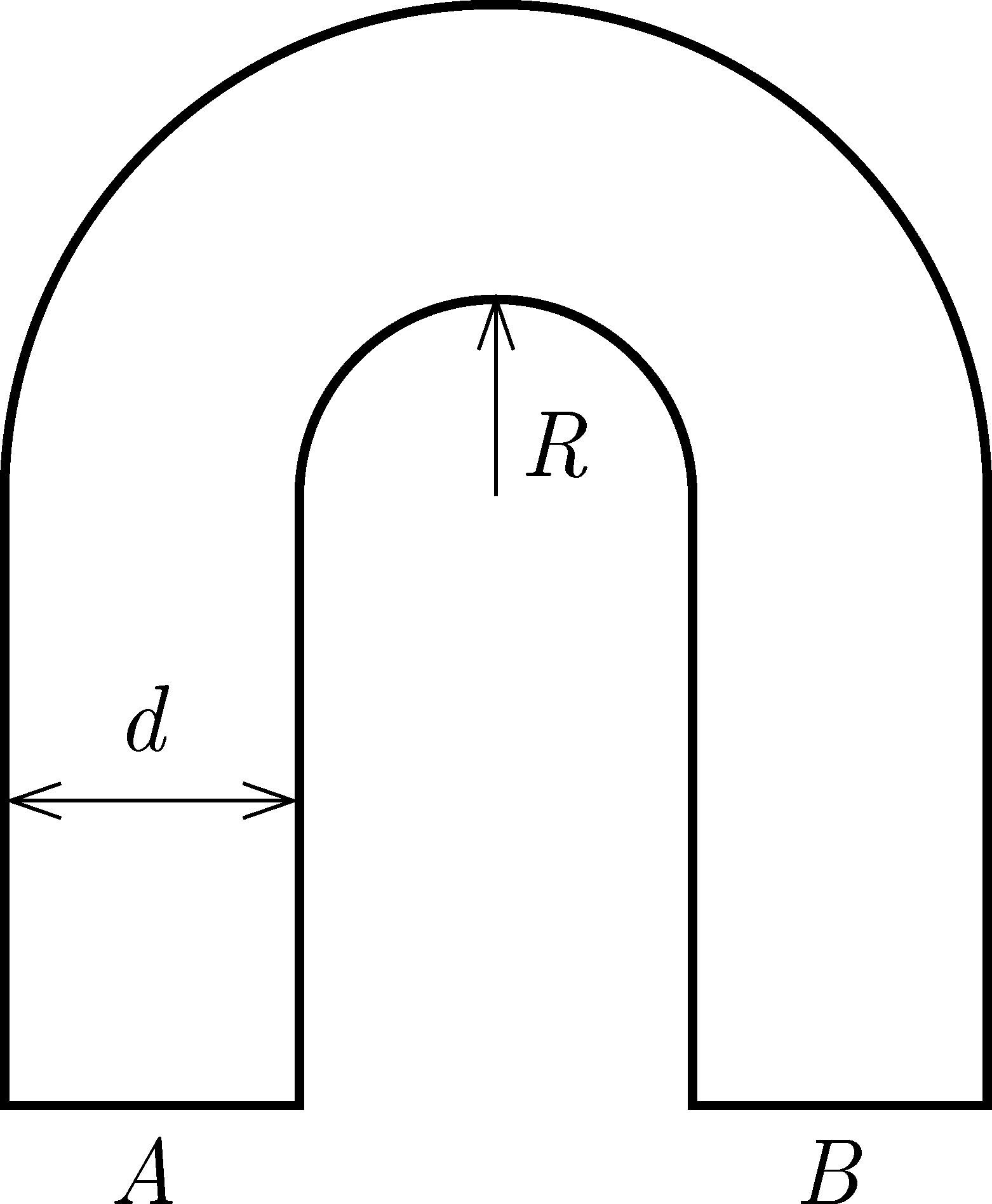
Közli: Honyek Gyula, Veresegyház
(4 pont)
A beküldési határidő 2024. október 15-én LEJÁRT.
Megoldás. Akkor fogja az \(\displaystyle A\) felületre érkező fény teljes egészében a \(\displaystyle B\) felületen elhagyni a meghajlított üvegrudat, ha ,,kanyargása'' közben mindig teljesen visszaverődik a rúd belső felületéről. Az ábra azt mutatja, hogy az A felület jobb szélén belépő fénysugár a kritikus.
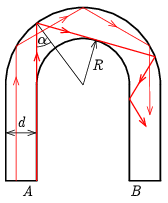
A teljes visszaverődés feltétele az, hogy a beesési szög ne legyen kisebb a határszögnél (\(\displaystyle \alpha\geq\alpha_{\mathrm{krit.}}\)):
\(\displaystyle \sin{\alpha}\geq\frac{1}{n},\)
ahol \(\displaystyle n=1{,}5\) az üveg törésmutatója. A félkört érintő sugarak geometriájából adódik, hogy
\(\displaystyle \sin{\alpha}=\frac{R}{R+d}.\)
Határesetben
\(\displaystyle \frac{R}{R+d}=\frac{1}{n},\)
vagyis
\(\displaystyle \left(\frac{R}{d}\right)_\mathrm{min}=\frac{1}{n-1}=\frac{1}{1{,}5-1}=2.\)
Megjegyzés: Egyszerű geometriai megfontolások alapján beláthatjuk, hogy ha az \(\displaystyle R/d\) arány legalább 2, akkor bármely fénysugár esetén, akármelyik további belső visszaverődésekor is teljes visszaverődés történik.
Statisztika:
26 dolgozat érkezett. 4 pontot kapott: Agócs Zoltán, Bélteki Teó, Bús László Teodor, Csiszár András, Domján Noémi Dóra, Fekete Lúcia, Kis Boglárka 08, Kiss 131 Adorján Timon, Klement Tamás, Kovács Dániel, Ligeti Barnabás, Masa Barnabás, Simon János Dániel, Sütő Áron, Tóth Hanga Katalin, Tóth Kolos Barnabás, Tóth-Tűri Bence, Ujpál Bálint, Vincze Anna. 3 pontot kapott: Pázmándi József Áron. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2024. szeptemberi fizika feladatai